Full solution
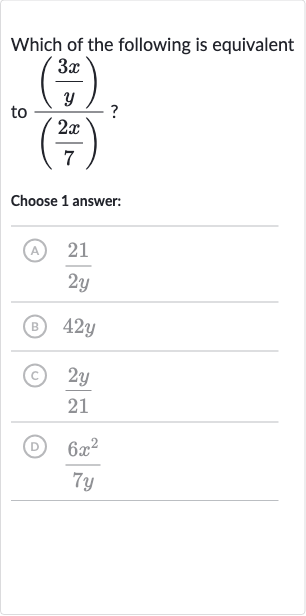
Q. Which of the following is equivalent to ?Choose answer:(A) (B) (C) (D)
- Problem Understanding: Understand the problem.We need to simplify the complex fraction .
- Rewriting the Complex Fraction: Rewrite the complex fraction as a division problem.The expression / can be rewritten as .
- Using the Rule for Dividing Fractions: Use the rule for dividing fractions.To divide by a fraction, multiply by its reciprocal. So, becomes .
- Simplifying the Expression: Simplify the expression.Now we multiply the numerators and the denominators: .This simplifies to .
- Canceling out Common Factors: Cancel out the common factors.We can cancel the in the numerator and the denominator: .This leaves us with .
- Checking the Answer Choices: Check the answer choices.We compare our simplified expression with the given options and find that it matches with option (A) .
More problems from Identify equivalent linear expressions I
QuestionGet tutor help