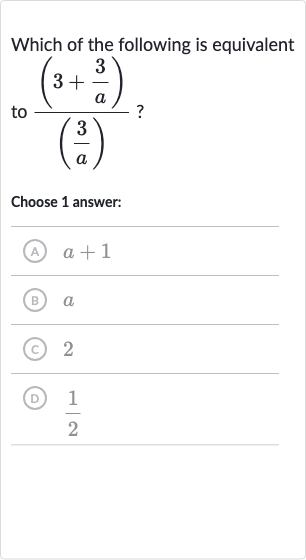
Which of the following is equivalent to ((3+(3)/(a)))/(((3)/(a))) ? Choose 1 answer: (A) a+1 (B) a (C) 2 (D) (1)/(2)

Question

Which of the following is equivalent to  ((3+(3)/(a)))/(((3)/(a))) ? Choose 1 answer: (A)  a+1 (B)  a (C) 2 (D)  (1)/(2)

Bytelearn · Accepted Answer

Simplify fractions: Simplify the numerator and the denominator. The expression given is ((3+(3)/(a)))/(((3)/(a))). We can start by simplifying the numerator and the denominator separately. The numerator is 3 + (3/a), which can be written as a single fraction by finding a common denominator. The denominator is (3/a), which is already a single fraction.Combine terms: Combine the terms in the numerator. To combine 3 and (3/a), we need a common denominator, which is 'a'. So we convert 3 to a fraction with the same denominator: 3 = (3a)/a Now we can add the two fractions: (3a)/a + (3/a) = (3a + 3)/aRewrite expression: Rewrite the original expression with the simplified numerator. Now that we have the simplified numerator, we can rewrite the original expression as: ((3a + 3)/a) / (3/a)Divide fractions: Divide the fractions. To divide fractions, we multiply the first fraction by the reciprocal of the second fraction: ((3a + 3)/a) * (a/3)Simplify expression: Simplify the expression. When we multiply the fractions, we can cancel out the 'a' in the numerator of the first fraction and the 'a' in the denominator of the second fraction: (3a + 3)/3Divide terms: Divide each term in the numerator by the denominator. Now we divide each term in the numerator by 3: (3a/3) + (3/3) This simplifies to: a + 1

Which of the following is equivalent to $\frac{\left(3+\frac{3}{a}\right)}{\left(\frac{3}{a}\right)}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $a+1$ $\newline$ (B) $a$ $\newline$ (C) $2$ $\newline$ (D) $\frac{1}{2}$

Full solution

More problems from Identify equivalent linear expressions

Related topics

Which of the following is equivalent to (3+3a)(3a) \frac{\left(3+\frac{3}{a}\right)}{\left(\frac{3}{a}\right)} (a3​)(3+a3​)​ ?\newlineChoose 111 answer:\newline(A) a+1 a+1 a+1\newline(B) a a a\newline(C) 222\newline(D) 12 \frac{1}{2} 21​

Which of the following is equivalent to $\frac{\left(3+\frac{3}{a}\right)}{\left(\frac{3}{a}\right)}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $a+1$ $\newline$ (B) $a$ $\newline$ (C) $2$ $\newline$ (D) $\frac{1}{2}$