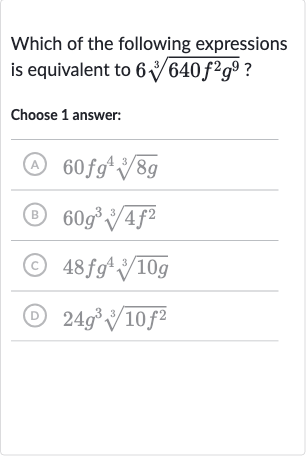
Which of the following expressions is equivalent to 6root(3)(640f^(2)g^(9)) ? Choose 1 answer: (A) 60 fg^(4)root(3)(8g) (B) 60g^(3)root(3)(4f^(2)) (c) 48 fg^(4)root(3)(10 g) (D) 24g^(3)root(3)(10f^(2))

Question

Which of the following expressions is equivalent to  6root(3)(640f^(2)g^(9)) ? Choose 1 answer: (A)  60 fg^(4)root(3)(8g) (B)  60g^(3)root(3)(4f^(2)) (c)  48 fg^(4)root(3)(10 g) (D)  24g^(3)root(3)(10f^(2))

Bytelearn · Accepted Answer

Simplify Expression: First, let's simplify the expression inside the cube root. 640 can be factored into prime factors: 640 = 2^7 * 5. The expression becomes 6root(3)(2^7 * 5 * f^2 * g^9).Split into Separate Roots: We can split the cube root into separate roots for each factor: 6 * root(3)(2^7) * root(3)(5) * root(3)(f^2) * root(3)(g^9).Simplify Each Cube Root: Now, we simplify each cube root separately. For root(3)(2^7), we can take out 2^2 (which is 4) from the cube root because 2^6 is a perfect cube. This leaves us with 6 * 4 * root(3)(2) * root(3)(5) * root(3)(f^2) * root(3)(g^9).Multiply Constants: For root(3)(g^9), g^9 is a perfect cube (since 9 is divisible by 3), so we can take g^3 out of the cube root. This gives us 6 * 4 * g^3 * root(3)(2) * root(3)(5) * root(3)(f^2).Combine Numbers Inside Root: For root(3)(f^2), we cannot simplify further since 2 is not divisible by 3. So, it remains inside the cube root.Compare with Answer Choices: Now, we multiply the constants outside the cube root: 6 * 4 * g^3 = 24g^3. The expression now is 24g^3 * root(3)(2 * 5 * f^2).We can combine the numbers inside the cube root: root(3)(2 * 5) = root(3)(10). The expression simplifies to 24g^3 * root(3)(10 * f^2).We compare the simplified expression with the answer choices. The expression 24g^3 * root(3)(10 * f^2) matches with choice (D).

Which of the following expressions is equivalent to $6 \sqrt[3]{640 f^{2} g^{9}}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $60 f g^{4} \sqrt[3]{8 g}$ $\newline$ (B) $60 g^{3} \sqrt[3]{4 f^{2}}$ $\newline$ (C) $48 f g^{4} \sqrt[3]{10 g}$ $\newline$ (D) $24 g^{3} \sqrt[3]{10 f^{2}}$

Full solution

More problems from Identify equivalent linear expressions I

Related topics