Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

When graphed in the
xy-plane, the function
f(x)=3(2)^(x)+1 has a
y-intercept at
(0,k). What is the value of
k ?
Choose 1 answer:
(A) 1
(B) 2
(c) 3
(D) 4

When graphed in the $x y$ -plane, the function $f(x)=3(2)^{x}+1$ has a $y$ -intercept at $(0, k)$ . What is the value of $k$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $1$ $\newline$ (B) $2$ $\newline$ (C) $3$ $\newline$ (D) $4$

View step-by-step help

View step-by-step help

Domain and range of quadratic functions: equations

Full solution

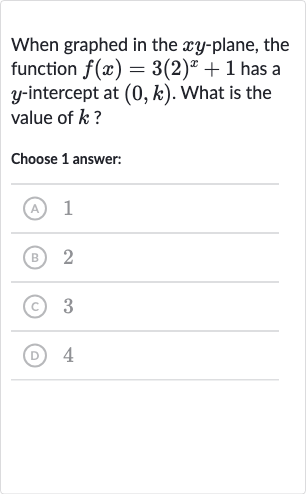
Q. When graphed in the

x y

-plane, the function

f(x)=3(2)^{x}+1

has a

y

-intercept at

(0, k)

. What is the value of

k

?

\newline

Choose

1

answer:

\newline

(A)

1

\newline

(B)

2

\newline

(C)

3

\newline

(D)

4

Evaluate at $x=0$ : To find the y-intercept of the function, we need to evaluate the function at $x = 0$ . The y-intercept occurs where the graph of the function crosses the y-axis, which is when $x = 0$ .
Substitute $x=0$ : Substitute $x = 0$ into the function $f(x) = 3(2)^x + 1$ to find the value of $k$ . $\newline$ $f(0) = 3(2)^0 + 1$
Calculate $2^0$ : Calculate the value of $2$ raised to the power of $0$ , which is $1$ . $\newline$ $2^0 = 1$
Multiply by $3$ : Multiply $3$ by the result from the previous step. $\newline$ $3 \times 1 = 3$
Add $1$ : Add $1$ to the result from the previous step to find the value of $f(0)$ , which is the y-intercept $k$ . $\newline$ $3 + 1 = 4$

More problems from Domain and range of quadratic functions: equations

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 8 months ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 7 months ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 5 months ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 5 months ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 5 months ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 5 months ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 5 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 4 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 4 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 5 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant