Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the missing constant term in the perfect square that starts with
x^(2)-8x ?

What is the missing constant term in the perfect square that starts with $x^{2}-8x$ ?

View step-by-step help

View step-by-step help

Solve a quadratic equation by completing the square

Full solution

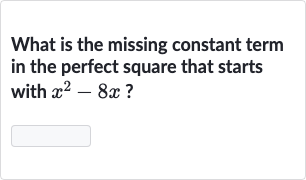
Q. What is the missing constant term in the perfect square that starts with

x^{2}-8x

?

Step $1$ : Identify the expression: To complete the square for an expression of the form $x^2 - bx$ , we need to find the value that makes it a perfect square trinomial. This value is found by taking $(\frac{b}{2})^2$ .
Step $2$ : Calculate the value of $\frac{b}{2}$ : In the expression $x^2 - 8x$ , the coefficient $b$ in front of $x$ is $-8$ . To find the constant term that completes the square, we calculate $\left(-\frac{8}{2}\right)^2$ .
Step $3$ : Square the value: Performing the calculation, we get $(-\frac{8}{2})^2 = (-4)^2 = 16$ .
Step $4$ : Add the constant term to the expression: The missing constant term that completes the square for the expression $x^2 - 8x$ is $16$ . Adding this term to the expression would give us a perfect square trinomial: $x^2 - 8x + 16$ .

More problems from Solve a quadratic equation by completing the square

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 11 months ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 10 months ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 8 months ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 8 months ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 8 months ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 8 months ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 8 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 7 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 7 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant