AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
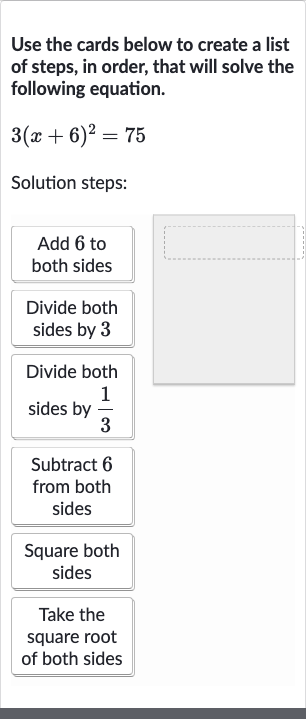
Use the cards below to create a list of steps, in order, that will solve the following equation.Solution steps:\text{Take the square root of both sides}
Full solution
Q. Use the cards below to create a list of steps, in order, that will solve the following equation.Solution steps:
- Isolate squared term: First, we need to isolate the squared term on one side of the equation. To do this, we divide both sides by .Calculation:
- Take square root: Next, we take the square root of both sides to solve for . Remember that taking the square root of both sides introduces a plus/minus ( can be + or -).Calculation:
- Isolate : Now, we need to isolate by subtracting from both sides of the equation.Calculation: or
- Simplify expressions: Finally, we simplify the expressions to find the two possible values for .Calculation: and
More problems from Solve a quadratic equation using square roots
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
