Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The sum of the first 6 terms of a geometric series is 15,624 and the common ratio is 5 .
What is the first term of the series?

The sum of the first $6$ terms of a geometric series is $15$ , $624$ and the common ratio is $5$ . $\newline$ What is the first term of the series?

View step-by-step help

View step-by-step help

Find the sum of a finite geometric series

Full solution

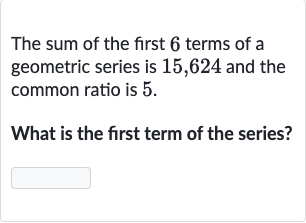
Q. The sum of the first

6

terms of a geometric series is

15

,

624

and the common ratio is

5

.

\newline

What is the first term of the series?

Formula Application: The sum of the first $n$ terms of a geometric series can be found using the formula $S_n = \frac{a(1 - r^n)}{(1 - r)}$ , where $S_n$ is the sum of the first $n$ terms, $a$ is the first term, $r$ is the common ratio, and $n$ is the number of terms. We are given that $S_6 = 15,624$ , $r = 5$ , and $n = 6$ . We need to solve for $a$ .
Plug Known Values: First, let's plug the known values into the formula for the sum of a geometric series: $\newline$ $S_6 = a(1 - 5^6) / (1 - 5)$ $\newline$ $15,624 = a(1 - 15625) / (1 - 5)$
Simplify Equation: Now, let's simplify the denominator and the numerator inside the parentheses: $\newline$ $15,624 = a(1 - 15625) / (-4)$ $\newline$ $15,624 = a(-15624) / (-4)$
Divide by Constant: Next, we simplify the right side of the equation by dividing $-15624$ by $-4$ : $15,624 = a(3906)$
Final Division: To find the value of $a$ , we divide both sides of the equation by $3906$ : $a = \frac{15,624}{3906}$
Find Value of a: Now, we perform the division to find the value of $a$ : $a = 4$

More problems from Find the sum of a finite geometric series

Question

Find the sum of the finite arithmetic series.

\sum_{n=1}^{10} (7n+4)

\newline

Posted 3 months ago

Question

Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`

Posted 2 months ago

Question

Type the missing number in this sequence: `2, 4 8`, ______,`32`

Posted 2 months ago

Question

What kind of sequence is this?

2, 10, 50, 250, \ldots

Choices:Choices:

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

What is the missing number in this pattern?

1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_

Posted 2 months ago

Question

Classify the series.

\sum_{n = 0}^{12} (n + 2)^3

\newline

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 6 + 11 + 16 + 21 + 26 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 2 months ago

Question

Find the third partial sum of the series.

\newline

3 + 9 + 15 + 21 + 27 + 33 + \cdots

\newline

Write your answer as an integer or a fraction in simplest form.

\newline

S_3 =

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 7 + 13 + 19 + 25 + 31 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 3 months ago

Question

Does the infinite geometric series converge or diverge?

\newline

1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots

\newline

\newline

\text{[A]converge}

\newline

\text{[B]diverge}

Posted 2 months ago