AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
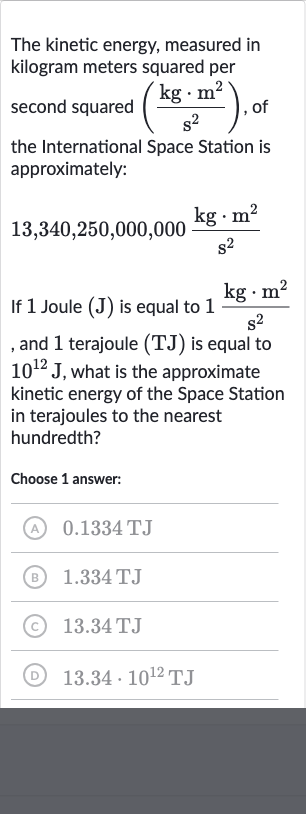
The kinetic energy, measured in kilogram meters squared per second squared , of the International Space Station is approximately:If Joule is equal to , and terajoule is equal to , what is the approximate kinetic energy of the Space Station in terajoules to the nearest hundredth?Choose answer:(A) (B) (C) (D)
Full solution
Q. The kinetic energy, measured in kilogram meters squared per second squared , of the International Space Station is approximately:If Joule is equal to , and terajoule is equal to , what is the approximate kinetic energy of the Space Station in terajoules to the nearest hundredth?Choose answer:(A) (B) (C) (D)
- Understand Joules and Terajoules: Understand the relationship between joules and terajoules. terajoule (TJ) is equal to joules (J).
- Convert Kinetic Energy: Convert the given kinetic energy from joules to terajoules.The given kinetic energy is , which is equivalent to .To convert to terajoules, divide by .
- Round to Nearest Terajoule: Round the result to the nearest hundredth of a terajoule. TJ rounded to the nearest hundredth is TJ.
More problems from Interpret parts of quadratic expressions: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
