Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

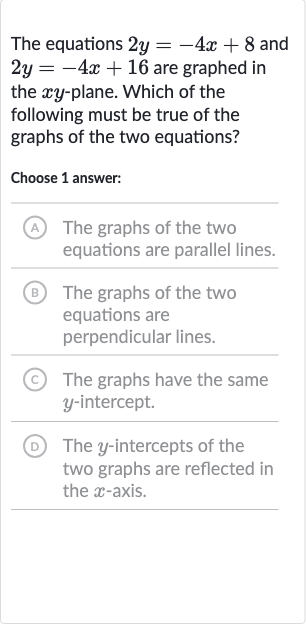
The equations 2y=-4x+8 and 2y=-4x+16 are graphed in the xy-plane. Which of the following must be true of the graphs of the two equations? Choose 1 answer: (A) The graphs of the two equations are parallel lines. (B) The graphs of the two equations are perpendicular lines. (c) The graphs have the same y-intercept. (D) The y-intercepts of the two graphs are reflected in the x-axis.

The equations 2y=−4x+8 2 y=-4 x+8 and 2y=−4x+16 2 y=-4 x+16 are graphed in the xy x y -plane. Which of the following must be true of the graphs of the two equations?\newlineChoose 11 answer:\newline(A) The graphs of the two equations are parallel lines.\newline(B) The graphs of the two equations are perpendicular lines.\newline(C) The graphs have the same y y -intercept.\newline(D) The y y -intercepts of the two graphs are reflected in the x x -axis.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Write a quadratic function from its x-intercepts and another pointright chevron icon

Full solution

Q. The equations 2y=−4x+8 2 y=-4 x+8 and 2y=−4x+16 2 y=-4 x+16 are graphed in the xy x y -plane. Which of the following must be true of the graphs of the two equations?\newlineChoose 11 answer:\newline(A) The graphs of the two equations are parallel lines.\newline(B) The graphs of the two equations are perpendicular lines.\newline(C) The graphs have the same y y -intercept.\newline(D) The y y -intercepts of the two graphs are reflected in the x x -axis.
  1. Equation Analysis: Let's analyze the first equation 2y=−4x+82y = -4x + 8. To find the slope and y-intercept, we can put it in slope-intercept form, which is y=mx+by = mx + b, where mm is the slope and bb is the y-intercept. Divide both sides by 22 to isolate yy. y=−2x+4y = -2x + 4 Here, the slope (mm) is −2-2 and the y-intercept (bb) is y=mx+by = mx + b00.
  2. Slope and Y-Intercept: Now let's analyze the second equation 2y=−4x+162y = -4x + 16. Again, we put it in slope-intercept form by dividing both sides by 22. y=−2x+8y = -2x + 8 Here, the slope (m)(m) is −2-2 and the y-intercept (b)(b) is 88.
  3. Comparison of Equations: Comparing the two equations, we see that they both have the same slope, −2-2, but different yy-intercepts, 44 and 88 respectively.\newlineSince they have the same slope, the lines are parallel to each other.
  4. Answer Choices: Now let's check the answer choices against our findings:\newline(A) The graphs of the two equations are parallel lines. This is true based on our analysis.\newline(B) The graphs of the two equations are perpendicular lines. This is false because perpendicular lines would have slopes that are negative reciprocals of each other.\newline(C) The graphs have the same yy-intercept. This is false because the yy-intercepts are 44 and 88.\newline(D) The yy-intercepts of the two graphs are reflected in the xx-axis. This is false because a reflection across the xx-axis would not change the xx-coordinate of the yy-intercept, but would change the sign of the yy-coordinate.

More problems from Write a quadratic function from its x-intercepts and another point

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 1 year ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 9 months ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 9 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 9 months ago

View all (106)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant