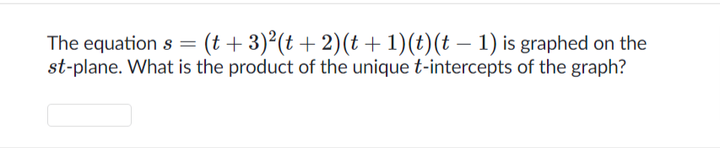Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The equation s=(t+3)^(2)(t+2)(t+1)(t)(t-1) is graphed on the st-plane. What is the product of the unique t-intercepts of the graph? ◻

The equation s=(t+3)2(t+2)(t+1)(t)(t−1) s=(t+3)^{2}(t+2)(t+1)(t)(t-1) is graphed on the st s t -plane. What is the product of the unique t t -intercepts of the graph?\newline□ \square

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Domain and range of quadratic functions: equationsright chevron icon

Full solution

Q. The equation s=(t+3)2(t+2)(t+1)(t)(t−1) s=(t+3)^{2}(t+2)(t+1)(t)(t-1) is graphed on the st s t -plane. What is the product of the unique t t -intercepts of the graph?\newline□ \square
  1. Identify t-intercepts: Identify the t-intercepts of the graph.\newlineThe t-intercepts occur when s=0s = 0. To find the t-intercepts, we set the equation equal to zero and solve for tt.\newline0=(t+3)2(t+2)(t+1)(t)(t−1)0 = (t+3)^{2}(t+2)(t+1)(t)(t-1)\newlineThe t-intercepts are the solutions to this equation.
  2. Find unique solutions for tt: Find the unique solutions for tt.\newlineThe equation is already factored, so we can see the solutions directly from the factors:\newlinet+3=0t+3 = 0 ⇒\Rightarrow t=−3t = -3 (this root is squared, but it still counts as one unique intercept)\newlinet+2=0t+2 = 0 ⇒\Rightarrow t=−2t = -2\newlinet+1=0t+1 = 0 ⇒\Rightarrow t=−1t = -1\newlinet=0t = 0 \newlinet−1=0t-1 = 0 ⇒\Rightarrow t=1t = 1\newlineThese are the unique t−t-intercepts of the graph.
  3. Calculate product of t-intercepts: Calculate the product of the unique t-intercepts.\newlineThe product of the t-intercepts is found by multiplying them together:\newlineProduct = (−3)×(−2)×(−1)×(0)×(1)(-3) \times (-2) \times (-1) \times (0) \times (1)
  4. Simplify the product: Simplify the product.\newlineSince one of the factors is 00, the product of the tt-intercepts is 00.\newlineProduct = 00

More problems from Domain and range of quadratic functions: equations

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 3 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 3 months ago

View all (37)