Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The common ratio in a geometric series is 0.5 and the first term is 256.
Find the sum of the first 6 terms in the series.

The common ratio in a geometric series is $0$ . $5$ and the first term is $256$ . $\newline$ Find the sum of the first $6$ terms in the series.

View step-by-step help

View step-by-step help

Find the sum of a finite geometric series

Full solution

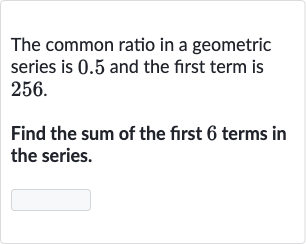
Q. The common ratio in a geometric series is

0

.

5

and the first term is

256

.

\newline

Find the sum of the first

6

terms in the series.

Question Prompt: The question prompt is: ＂Find the sum of the first $6$ terms in a geometric series with a common ratio of $0.5$ and a first term of $256$ .＂
Formula for Sum: To find the sum of the first $6$ terms of a geometric series, we use the formula for the sum of the first n terms of a geometric series, which is $S_n = \frac{a(1 - r^n)}{1 - r}$ , where $S_n$ is the sum of the first n terms, $a$ is the first term, $r$ is the common ratio, and $n$ is the number of terms.
Substitute Values: Substitute the given values into the formula: $a = 256$ , $r = 0.5$ , and $n = 6$ . So, $S_6 = \frac{256(1 - (0.5)^6)}{1 - 0.5}$ .
Calculate Power: Calculate the value of $(0.5)^6$ . This equals $0.5^6 = 0.015625$ .
Substitute Back: Substitute the value of $(0.5)^6$ back into the formula: $S_6 = \frac{256(1 - 0.015625)}{1 - 0.5}$ .
Simplify Expression: Simplify the expression inside the parentheses and the denominator: $S_6 = \frac{256(0.984375)}{0.5}$ .
Perform Operations: Perform the multiplication and division to find $S_6$ : $S_6 = \frac{256 \times 0.984375}{0.5} = 512$ .

More problems from Find the sum of a finite geometric series

Question

Find the sum of the finite arithmetic series.

\sum_{n=1}^{10} (7n+4)

\newline

Posted 2 months ago

Question

Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`

Posted 1 month ago

Question

Type the missing number in this sequence: `2, 4 8`, ______,`32`

Posted 2 months ago

Question

What kind of sequence is this?

2, 10, 50, 250, \ldots

Choices:Choices:

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

What is the missing number in this pattern?

1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_

Posted 1 month ago

Question

Classify the series.

\sum_{n = 0}^{12} (n + 2)^3

\newline

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 1 month ago

Question

Find the first three partial sums of the series.

\newline

1 + 6 + 11 + 16 + 21 + 26 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 1 month ago

Question

Find the third partial sum of the series.

\newline

3 + 9 + 15 + 21 + 27 + 33 + \cdots

\newline

Write your answer as an integer or a fraction in simplest form.

\newline

S_3 =

Posted 1 month ago

Question

Find the first three partial sums of the series.

\newline

1 + 7 + 13 + 19 + 25 + 31 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 2 months ago

Question

Does the infinite geometric series converge or diverge?

\newline

1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots

\newline

\newline

\text{[A]converge}

\newline

\text{[B]diverge}

Posted 1 month ago