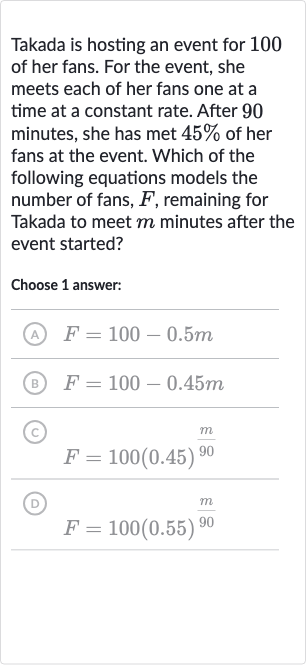
Takada is hosting an event for $100$ of her fans. For the event, she meets each of her fans one at a time at a constant rate. After $90$ minutes, she has met $45 \%$ of her fans at the event. Which of the following equations models the number of fans, $F$ , remaining for Takada to meet $m$ minutes after the event started? $\newline$ Choose $1$ answer: $\newline$ (A) $F=100-0.5 m$ $\newline$ (B) $F=100-0.45 m$ $\newline$ (C) $F=100(0.45)^{\frac{m}{90}}$ $\newline$ (D) $F=100(0.55)^{\frac{m}{90}}$

View step-by-step help

Home

Math Problems

Algebra 1

Solve a system of equations using any method: word problems

Full solution

Q. Takada is hosting an event for

100

of her fans. For the event, she meets each of her fans one at a time at a constant rate. After

90

minutes, she has met

45 \%

of her fans at the event. Which of the following equations models the number of fans,

F

, remaining for Takada to meet

m

minutes after the event started?

\newline

Choose

1

answer:

\newline

(A)

F=100-0.5 m

\newline

(B)

F=100-0.45 m

\newline

(C)

F=100(0.45)^{\frac{m}{90}}

\newline

(D)

F=100(0.55)^{\frac{m}{90}}

Calculate total fans met: Takada has met $45\%$ of her fans after $90$ minutes. To find the rate at which she meets her fans, we can calculate the number of fans she meets per minute.
Calculate rate of meeting fans: First, we calculate the total number of fans she has met in $90$ minutes. Since she has met $45\%$ of her $100$ fans, we multiply $100$ by $0.45$ . $\newline$ $100$ fans $\times 0.45 = 45$ fans
Create equation for remaining fans: Now, we find the rate by dividing the number of fans she has met by the time in minutes. $\newline$ Rate = $\frac{\text{Number of fans met}}{\text{Time in minutes}}$ $\newline$ Rate = $\frac{45 \text{ fans}}{90 \text{ minutes}} = 0.5 \text{ fans per minute}$
Match equation with answer choices: We can now create an equation to model the number of fans remaining, $F$ , after $m$ minutes. Since she meets $0.5$ fans per minute, we can multiply the rate by the time, $m$ , and subtract from the total number of fans. $\newline$ $F = \text{Total fans} - (\text{Rate} \times \text{Time})$ $\newline$ $F = 100 - (0.5 \times m)$
Match equation with answer choices: We can now create an equation to model the number of fans remaining, $F$ , after $m$ minutes. Since she meets $0.5$ fans per minute, we can multiply the rate by the time, $m$ , and subtract from the total number of fans. $\newline$ $F = \text{Total fans} - (\text{Rate} \times \text{Time})$ $\newline$ $F = 100 - (0.5 \times m)$ $\newline$ Looking at the answer choices, we see that option (A) matches our equation. $\newline$ $F = 100 - 0.5 m$