Full solution
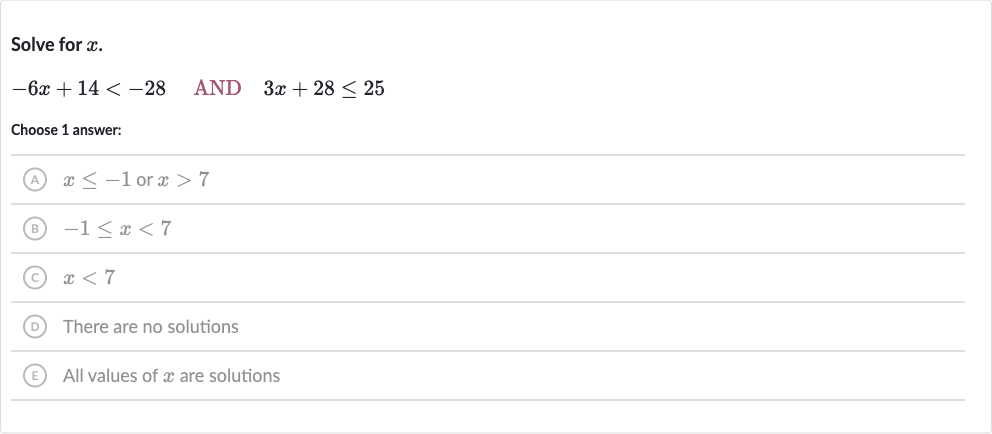
Q. Solve for . AND Choose answer:(A) or (B) (C) (D) There are no solutions(E) All values of are solutions
- Solving the first inequality: First, let's solve the first inequality -6x + 14 < -28.Subtract from both sides to isolate the term with .-6x + 14 - 14 < -28 - 14-6x < -42Now, divide both sides by , remembering to reverse the inequality sign because we are dividing by a negative number.x > 7
- Solving the second inequality: Next, let's solve the second inequality .Subtract from both sides to isolate the term with .Now, divide both sides by to solve for .
- Considering the two inequalities: Now we have two inequalities to consider: x > 7 from the first inequality and from the second inequality.These two inequalities do not overlap; there is no value of that can satisfy both conditions simultaneously.Therefore, there are no solutions to the system of inequalities.
More problems from Is (x, y) a solution to the system of linear inequalities?
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help