Full solution
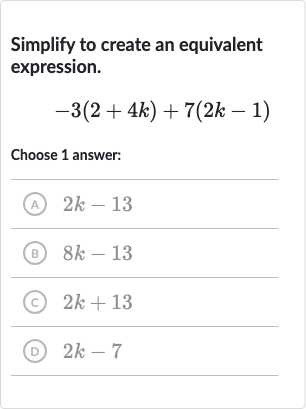
Q. Simplify to create an equivalent expression.Choose answer:(A) (B) (C) (D)
- Distribute terms in parentheses: Distribute to each term inside the first parentheses and to each term inside the second parentheses. becomes . becomes .
- Combine like terms: Combine like terms from the distributed expressions.
- Simplify the expression: Combine the constant terms and ) and the terms and ).So, the expression simplifies to .
More problems from Simplify variable expressions involving like terms and the distributive property
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help