AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
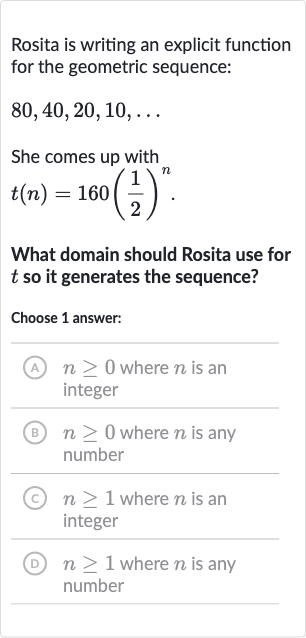
Rosita is writing an explicit function for the geometric sequence:She comes up withWhat domain should Rosita use for so it generates the sequence?Choose answer:(A) where is an integer(B) where is any number(C) where is an integer(D) where is any number
Full solution
Q. Rosita is writing an explicit function for the geometric sequence:She comes up withWhat domain should Rosita use for so it generates the sequence?Choose answer:(A) where is an integer(B) where is any number(C) where is an integer(D) where is any number
- Step : Plugging in : Rosita's function for the geometric sequence is . To determine the domain, we need to see which values of will generate the sequence and so on. Let's start by plugging in to see if we get the first term of the sequence, which is .
- Step : Checking for : Since , which is the first term of the sequence, we can see that the sequence starts with . Now let's check if the function works for to get the second term of the sequence, which is .
- Step : Testing non-integer value: The function also works for , giving us the second term of the sequence. This suggests that the domain should start at . Now let's check if the function only works for integer values of by trying a non-integer value, such as .
This result is not an integer and does not correspond to any term in the geometric sequence. - Step : Determining the domain: Since the function does not produce terms of the geometric sequence for non-integer values of , we can conclude that the domain should only include integer values of . Therefore, the domain should be where is an integer.
