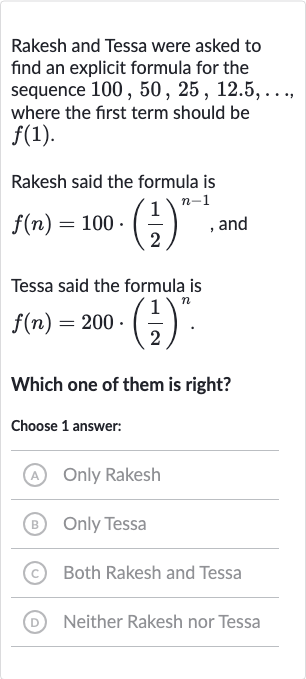
Rakesh and Tessa were asked to find an explicit formula for the sequence $\newline$ $100, 50, 25, 12.5, \dots$ , where the first term should be $\newline$ $f(1)$ . $\newline$ Rakesh said the formula is $\newline$ $f(n) = 100 \left(\frac{1}{2}\right)^{n-1}$ , and $\newline$ Tessa said the formula is $\newline$ $f(n) = 200 \left(\frac{1}{2}\right)^n$ . $\newline$ Which one of them is right? $\newline$ Choose $1$ answer: $\newline$ (A) Only Rakesh $\newline$ (B) Only Tessa $\newline$ (C) Both Rakesh and Tessa $\newline$ (D) Neither Rakesh nor Tessa

View step-by-step help

Home

Math Problems

Algebra 1

Write variable expressions for geometric sequences

Full solution

Q. Rakesh and Tessa were asked to find an explicit formula for the sequence

\newline

100, 50, 25, 12.5, \dots

, where the first term should be

\newline

f(1)

\newline

Rakesh said the formula is

\newline

f(n) = 100 \left(\frac{1}{2}\right)^{n-1}

, and

\newline

Tessa said the formula is

\newline

f(n) = 200 \left(\frac{1}{2}\right)^n

\newline

Which one of them is right?

\newline

Choose

1

answer:

\newline

(A) Only Rakesh

\newline

(B) Only Tessa

\newline

\newline

(D) Neither Rakesh nor Tessa

Identify the pattern: We have the sequence: $100, 50, 25, 12.5, extellipsis$ Identify the pattern in the sequence. Each term is half of the previous term, which indicates that this is a geometric sequence with a common ratio of $\frac{1}{2}$ .
Determine first term and common ratio: Determine the first term ( $f(1)$ ) and the common ratio ( $r$ ) of the sequence. $\newline$ First term: $f(1) = 100$ $\newline$ Common ratio: $r = \frac{50}{100} = \frac{1}{2}$
Use the formula for the nth term: Using the formula for the nth term of a geometric sequence, which is $f(n) = a \cdot r^{(n - 1)}$ , where $a$ is the first term and $r$ is the common ratio. $\newline$ Substitute $100$ for $a$ and $\frac{1}{2}$ for $r$ to get Rakesh's formula. $\newline$ $f(n) = 100 \cdot \left(\frac{1}{2}\right)^{(n - 1)}$
Check Tessa's formula: Now, let's check Tessa's formula. $\newline$ According to Tessa, $f(n) = 200 \times \left(\frac{1}{2}\right)^n$ . $\newline$ To verify this, let's calculate the first term using Tessa's formula: $\newline$ $f(1) = 200 \times \left(\frac{1}{2}\right)^1 = 200 \times \frac{1}{2} = 100$ $\newline$ This is correct for the first term, but let's check the second term: $\newline$ $f(2) = 200 \times \left(\frac{1}{2}\right)^2 = 200 \times \frac{1}{4} = 50$ $\newline$ This is also correct for the second term. However, Tessa's formula does not follow the standard form of a geometric sequence formula, which is $f(n) = a \times r^{(n - 1)}$ . Instead, it seems to be shifted by one position.
Compare both formulas: Compare both formulas to determine which one is correct. $\newline$ Rakesh's formula is in the standard form of a geometric sequence and correctly calculates the terms of the sequence. $\newline$ Tessa's formula also calculates the terms of the sequence correctly, but it is not in the standard form. It is equivalent to Rakesh's formula if we consider it as $f(n) = 100 \times (\frac{1}{2})^{(n - 1 + 1)}$ , which simplifies to $f(n) = 100 \times (\frac{1}{2})^{n}$ .
Conclude the correct answer: Conclude which answer is correct based on the standard form of the geometric sequence formula. Rakesh's formula is in the standard form and is correct. Tessa's formula, although not in the standard form, is mathematically equivalent to Rakesh's formula and also correctly describes the sequence. Therefore, both Rakesh and Tessa are correct.