Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

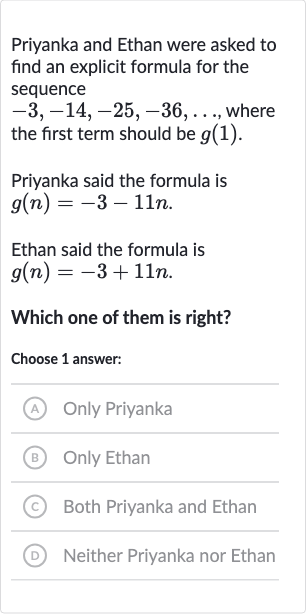
Priyanka and Ethan were asked to find an explicit formula for the sequence -3,-14,-25,-36,dots, where the first term should be g(1). Priyanka said the formula is g(n)=-3-11 n. Ethan said the formula is g(n)=-3+11 n. Which one of them is right? Choose 1 answer: (A) Only Priyanka (B) Only Ethan (c) Both Priyanka and Ethan (D) Neither Priyanka nor Ethan

Priyanka and Ethan were asked to find an explicit formula for the sequence −3,−14,−25,−36,… -3,-14,-25,-36, \ldots , where the first term should be g(1) g(1) .\newlinePriyanka said the formula is g(n)=−3−11n g(n)=-3-11 n .\newlineEthan said the formula is g(n)=−3+11n g(n)=-3+11 n .\newlineWhich one of them is right?\newlineChoose 11 answer:\newline(A) Only Priyanka\newline(B) Only Ethan\newline(C) Both Priyanka and Ethan\newline(D) Neither Priyanka nor Ethan

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Write a formula for an arithmetic sequenceright chevron icon

Full solution

Q. Priyanka and Ethan were asked to find an explicit formula for the sequence −3,−14,−25,−36,… -3,-14,-25,-36, \ldots , where the first term should be g(1) g(1) .\newlinePriyanka said the formula is g(n)=−3−11n g(n)=-3-11 n .\newlineEthan said the formula is g(n)=−3+11n g(n)=-3+11 n .\newlineWhich one of them is right?\newlineChoose 11 answer:\newline(A) Only Priyanka\newline(B) Only Ethan\newline(C) Both Priyanka and Ethan\newline(D) Neither Priyanka nor Ethan
  1. Question Prompt: The question_prompt: Determine which explicit formula correctly represents the sequence −3,−14,−25,−36,…-3, -14, -25, -36, \ldots, where the first term is g(1)g(1).
  2. Find Common Difference: To find the correct formula, we need to determine the common difference in the sequence. We can do this by subtracting the first term from the second term.\newlineCommon difference = second term - first term = −14−(−3)=−14+3=−11-14 - (-3) = -14 + 3 = -11.
  3. Write General Formula: Now that we have the common difference, we can write the general formula for an arithmetic sequence as:\newlineg(n)=first term+(n−1)×common differenceg(n) = \text{first term} + (n - 1) \times \text{common difference}.\newlineSubstituting the known values, we get:\newlineg(n)=−3+(n−1)×(−11)g(n) = -3 + (n - 1) \times (-11).
  4. Simplify Formula: Simplify the formula: g(n)=−3−11×(n−1)g(n) = -3 - 11 \times (n - 1). Distribute the −11-11: g(n)=−3−11n+11g(n) = -3 - 11n + 11.
  5. Compare Formulas: Combine like terms: g(n)=8−11ng(n) = 8 - 11n. This is the correct formula for the given sequence.
  6. Priyanka's Formula: Now, let's compare the correct formula with the formulas provided by Priyanka and Ethan:\newlinePriyanka's formula: g(n)=−3−11ng(n) = -3 - 11n.\newlineEthan's formula: g(n)=−3+11ng(n) = -3 + 11n.
  7. Ethan's Formula: We can see that Priyanka's formula matches the correct formula we derived, which is g(n)=8−11ng(n) = 8 - 11n, if we consider that the constant term 88 is not necessary for the sequence pattern and only affects the starting point. Therefore, Priyanka's formula correctly represents the sequence pattern.\newlineEthan's formula, however, has a positive 11n11n instead of a negative 11n11n, which does not match the pattern of the sequence.

More problems from Write a formula for an arithmetic sequence

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 5 months ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 5 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 5 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 7 months ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 9 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 5 months ago

View all (93)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant