Full solution
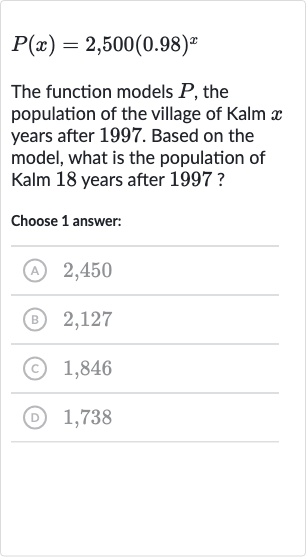
Q. The function models , the population of the village of Kalm years after . Based on the model, what is the population of Kalm years after ?Choose answer:(A) ,(B) ,(C) ,(D) ,
- Identify Function and Value: Identify the given function and the value to substitute for .The function given is , which models the population of the village of Kalm years after . We need to find the population years after , so we will substitute with .
- Substitute with : Substitute with in the function to calculate the population.
- Calculate : Calculate the value of . Using a calculator, we find that .
- Multiply by ,: Multiply the result from Step by to find the population.
- Round to Nearest Whole Number: Round the result to the nearest whole number, as population is typically expressed as a whole number.