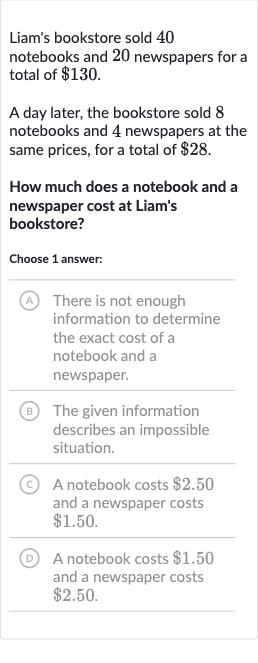
Liam's bookstore sold 40 notebooks and 20 newspapers for a total of $130. A day later, the bookstore sold 8 notebooks and 4 newspapers at the same prices, for a total of $28. How much does a notebook and a newspaper cost at Liam's bookstore? Choose 1 answer: (A) There is not enough information to determine the exact cost of a notebook and a newspaper. (B) The given information describes an impossible situation. (C) A notebook costs $2.50 and a newspaper costs $1.50. (D) A notebook costs $1.50 and a newspaper costs $2.50.

Question

Liam's bookstore sold 40 notebooks and 20 newspapers for a total of  $130. A day later, the bookstore sold 8 notebooks and 4 newspapers at the same prices, for a total of  $28. How much does a notebook and a newspaper cost at Liam's bookstore? Choose 1 answer: (A) There is not enough information to determine the exact cost of a notebook and a newspaper. (B) The given information describes an impossible situation. (C) A notebook costs  $2.50 and a newspaper costs  $1.50. (D) A notebook costs  $1.50 and a newspaper costs  $2.50.

Bytelearn · Accepted Answer

Equation setup: Set up the system of equations based on the information given. The first equation comes from the first day's sales: 40 notebooks and 20 newspapers for $130. Let n be the cost of a notebook and p be the cost of a newspaper. 40n + 20p = 130First day's sales: Set up the second equation from the second day's sales: 8 notebooks and 4 newspapers for $28. 8n + 4p = 28Second day's sales: Simplify the second equation to make the coefficients more manageable. Divide the entire equation by 4. 2n + p = 7Simplify second equation: Multiply the simplified second equation by 20 to match the coefficient of p in the first equation. 20(2n + p) = 20(7) 40n + 20p = 140Match coefficients: Subtract the first equation from the modified second equation to solve for n. (40n + 20p) - (40n + 20p) = 140 - 130 0n + 0p = 10 This step results in an incorrect equation that implies 0 = 10, which is not possible.

Full solution

More problems from Solve a system of equations using any method: word problems

Related topics