Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

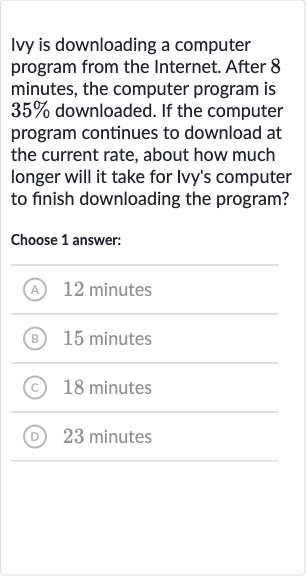
Ivy is downloading a computer program from the Internet. After 8 minutes, the computer program is 35% downloaded. If the computer program continues to download at the current rate, about how much longer will it take for Ivy's computer to finish downloading the program? Choose 1 answer: (A) 12 minutes (B) 15 minutes (C) 18 minutes (D) 23 minutes

Ivy is downloading a computer program from the Internet. After 88 minutes, the computer program is 35% 35 \% downloaded. If the computer program continues to download at the current rate, about how much longer will it take for Ivy's computer to finish downloading the program?\newlineChoose 11 answer:\newline(A) 1212 minutes\newline(B) 15 \mathbf{1 5} minutes\newline(C) 1818 minutes\newline(D) 2323 minutes

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Solve a system of equations using any method: word problemsright chevron icon

Full solution

Q. Ivy is downloading a computer program from the Internet. After 88 minutes, the computer program is 35% 35 \% downloaded. If the computer program continues to download at the current rate, about how much longer will it take for Ivy's computer to finish downloading the program?\newlineChoose 11 answer:\newline(A) 1212 minutes\newline(B) 15 \mathbf{1 5} minutes\newline(C) 1818 minutes\newline(D) 2323 minutes
  1. Calculate Percentage Remaining: Determine the percentage of the program that is still needed to be downloaded.\newlineSince 35%35\% of the program has been downloaded in 88 minutes, the remaining percentage to be downloaded is 100%−35%=65%100\% - 35\% = 65\%.
  2. Calculate Rate of Download: Calculate the rate of download per minute.\newlineTo find the rate, we divide the percentage downloaded by the time taken so far.\newlineRate = 35% downloaded8 minutes=4.375%\frac{35\% \text{ downloaded}}{8 \text{ minutes}} = 4.375\% per minute.
  3. Calculate Time Needed: Calculate the time needed to download the remaining 65%65\% at the rate of 4.375%4.375\% per minute.\newlineTime needed = Remaining percentage to download / Rate of download per minute\newlineTime needed = 65%/4.375%65\% / 4.375\% per minute ≈14.857\approx 14.857 minutes.
  4. Round to Nearest Whole Number: Round the time to the nearest whole number since the answer choices are in whole minutes.\newlineThe time needed is approximately 1515 minutes when rounded to the nearest whole number.

More problems from Solve a system of equations using any method: word problems

Question
Solve using elimination.\newlinex+6y=−15x + 6y = -15\newline−2x+6y=12-2x + 6y = 12\newline(_,_)(\_,\_)
Get tutor helpright-arrow

Posted 5 months ago

Question
Is (1,1)(1,1) a solution to this system of equations?\newline8x+y=98x + y = 9\newline6x+12y=186x + 12y = 18\newlineChoices:\newline[[yes]\newline[no]]
Get tutor helpright-arrow

Posted 5 months ago

Question
How many solutions does the system of equations below have?\newliney = x − 77\newliney = x − 77\newlineChoices:\newline[A]no solution\text{[A]no solution}\newline[B]one solution\text{[B]one solution}\newline[C]infinitely many solutions\text{[C]infinitely many solutions}
Get tutor helpright-arrow

Posted 7 months ago

Question
Which describes the system of equations below?\newliney=17x−10y = \frac{1}{7}x - 10\newliney=17x−10y = \frac{1}{7}x - 10\newlineChoices:\newline[A]consistent and independent\text{[A]consistent and independent}\newline[B]consistent and dependent\text{[B]consistent and dependent}\newline[C]inconsistent\text{[C]inconsistent}
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve using substitution.\newliney=−5y = -5\newline−4x+3y=17-4x + 3y = 17\newline(_____, _____)
Get tutor helpright-arrow

Posted 5 months ago

Question
Write a system of equations to describe the situation below, solve using substitution, and fill in the blanks.\newlineLast Wednesday, two friends met up after school to read the book they were both assigned in Literature class. Bryan can read 22 pages per minute, and he had already read 9898 pages. Jayla, who has a reading speed of 33 pages per minute, had read 4848 pages. Eventually they had read the same number of pages. How long did that take? How many pages had each of them read?\newlineAfter ____\_\_\_\_ minutes, Bryan and Jayla had each read ____\_\_\_\_ pages.
Get tutor helpright-arrow

Posted 5 months ago

Question
Write a system of equations to describe the situation below, solve using elimination, and fill in the blanks.\newlineAt the Castroville Ice Cream Parlor, one group of friends ordered 11 small serving of ice cream and 33 large servings of ice cream for 2020. Another group of friends ordered 11 small serving of ice cream and 44 large servings of ice cream for 2626. How much does the ice cream cost?\newlineThe ice cream costs `\$`_____ for a small serving and `\$`_____ for a large serving.
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve.\newliney=−1y = -1\newline−2x−4y=8-2x - 4y = 8\newline(_____ , _____)
Get tutor helpright-arrow

Posted 7 months ago

Question
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.\newlineThere are two mystery numbers. The sum of 33 times the first number and 33 times the second number is −18-18. The sum of 22 times the first number and 33 times the second number is −13-13. What are the two numbers?\newlineThe first number is ______ , and the second number is ______.
Get tutor helpright-arrow

Posted 7 months ago

Question
A teacher purchased 300300 colored pencils for an upcoming project. The pencils she ordered come in packs of 2020 and packs of 3030. She ordered 1414 packs in all. Write a system of equations to find the number of 2020-pencil packs (x)(x) and 3030-pencil packs (y)(y) the art teacher ordered.
Get tutor helpright-arrow

Posted 8 months ago

View all (187)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant