Full solution
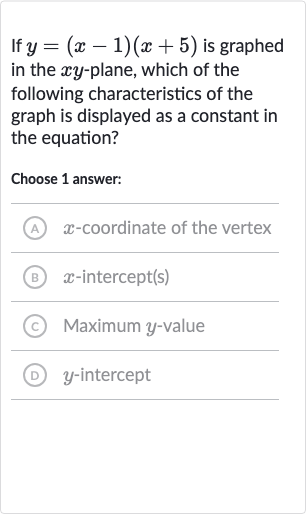
Q. If is graphed in the -plane, which of the following characteristics of the graph is displayed as a constant in the equation?Choose answer:(A) -coordinate of the vertex(B) -intercept(s)(C) Maximum -value(D) -intercept
- Understanding Standard Form: To find the characteristic of the graph that is displayed as a constant in the equation, we need to understand the standard form of a quadratic equation, which is . The constant term in this form is '', which represents the -intercept of the graph.
- Identifying the Constant Term: Let's identify the constant term in the given equation . To do this, we need to expand the equation.The constant term here is ''.
- Interpreting the Constant Term: The constant term '' in the expanded form of the equation represents the y-intercept of the graph. This is the point where the graph crosses the y-axis.
- Characteristics of the Graph: The -coordinate of the vertex, -intercepts, and maximum -value are not constants in the equation; they depend on the values of '', '', and '' and the shape of the parabola. However, the -intercept is directly given by the constant term '' in the equation .
More problems from Domain and range of quadratic functions: equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help