AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
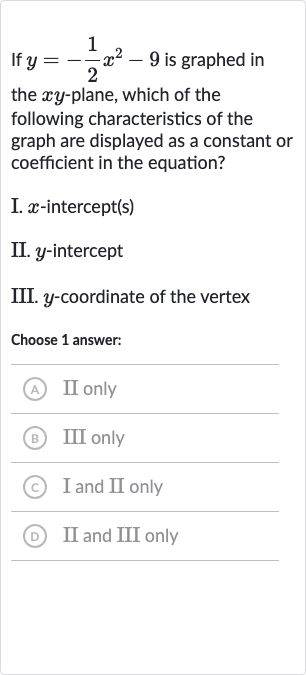
If is graphed in the -plane, which of the following characteristics of the graph are displayed as a constant or coefficient in the equation?I. -intercept(s)II. -interceptIII. -coordinate of the vertexChoose answer:(A) II only(B) III only(C) I and II only(D) II and III only
Full solution
Q. If is graphed in the -plane, which of the following characteristics of the graph are displayed as a constant or coefficient in the equation?I. -intercept(s)II. -interceptIII. -coordinate of the vertexChoose answer:(A) II only(B) III only(C) I and II only(D) II and III only
- Given quadratic function: The given quadratic function is . We need to identify which characteristics of the graph are displayed as a constant or coefficient in the equation.
- Y-intercept: The -intercept of a quadratic function in standard form is the constant term when . In this case, the constant term is , which means the -intercept is at .
- Vertex coordinates: The -coordinate of the vertex of a quadratic function in standard form can be found using the formula for the -coordinate of the vertex, and then substituting this value back into the function to find the -coordinate. However, since there is no term in this equation (), the -coordinate of the vertex is . Substituting into the equation gives us the -coordinate of the vertex, which is . This means the -coordinate of the vertex is also represented by the constant term .
- X-intercepts: The -intercepts (or roots) of the quadratic function are not directly displayed as a constant or coefficient in the equation. They would need to be calculated by setting and solving for , which is not represented by a specific term in the given equation.
- Characteristics displayed in equation: Based on the analysis, the -intercept and the -coordinate of the vertex are displayed as constants or coefficients in the equation, while the -intercepts are not. Therefore, the correct answer is II and III only.
