Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

If theta=(4pi)/(9) radians, what is the value of theta in degrees? Choose 1 answer: (A) 20^(@) (B) 36^(@) (c) 80^(@) (D) 720^(@)

If θ=4π9 \theta=\frac{4 \pi}{9} radians, what is the value of θ \theta in degrees?\newlineChoose 11 answer:\newline(A) 20∘ 20^{\circ} \newline(B) 36∘ 36^{\circ} \newline(C) 80∘ 80^{\circ} \newline(D) 720∘ 720^{\circ}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Inverses of sin, cos, and tan: degreesright chevron icon

Full solution

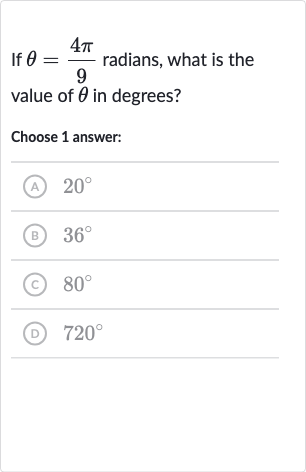
Q. If θ=4π9 \theta=\frac{4 \pi}{9} radians, what is the value of θ \theta in degrees?\newlineChoose 11 answer:\newline(A) 20∘ 20^{\circ} \newline(B) 36∘ 36^{\circ} \newline(C) 80∘ 80^{\circ} \newline(D) 720∘ 720^{\circ}
  1. Conversion factor for radians to degrees: To convert radians to degrees, we use the conversion factor that π\pi radians is equal to 180180 degrees. Therefore, we multiply the given radian measure by 180π\frac{180}{\pi} to convert it to degrees.\newlineCalculation: θ\theta in degrees = θ\theta in radians ×(180π)\times \left(\frac{180}{\pi}\right)\newlineθ\theta in degrees = (4π9)×(180π)\left(\frac{4\pi}{9}\right) \times \left(\frac{180}{\pi}\right)
  2. Calculation of θ\theta in degrees: Now, we simplify the expression by canceling out the π\pi in the numerator and the denominator.\newlineCalculation: θ\theta in degrees = (49)×180\left(\frac{4}{9}\right) \times 180
  3. Simplification of the expression: Next, we multiply 44 by 180180 and then divide by 99 to find the value of θ\theta in degrees.\newlineCalculation: θ\theta in degrees = (4×180)/9(4 \times 180) / 9\newlineθ\theta in degrees = 720/9720 / 9
  4. Calculation of θ\theta in degrees: Finally, we perform the division to get the value of θ\theta.\newlineCalculation: θ\theta in degrees = 7209\frac{720}{9}\newlineθ\theta in degrees = 8080

More problems from Inverses of sin, cos, and tan: degrees

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 2 months ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 2 months ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 3 months ago

View all (28)