Full solution
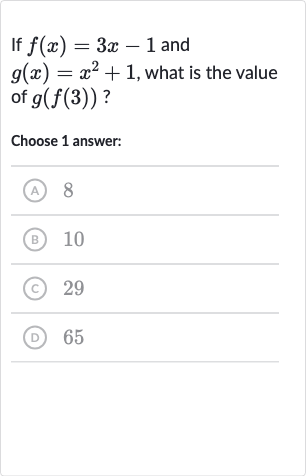
Q. If and , what is the value of ?Choose answer:(A) (B) (C) (D)
- Find : Given the functions and , we first need to find the value of .
- Substitute into : Now that we have , we need to find the value of , which means we need to substitute in with the value of .