AI tutor
Full solution
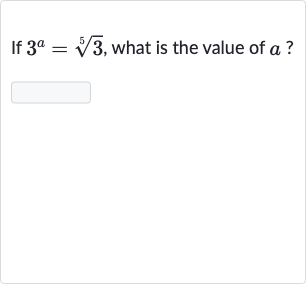
Q. If , what is the value of ?
- Given Equation: We are given the equation , which means that raised to the power of is equal to the fifth root of . To find the value of , we need to express both sides of the equation in a way that allows us to compare the exponents directly.
- Rewriting Equation: The fifth root of can be written as . So, we can rewrite the equation as .
- Setting Exponents Equal: Since the bases are the same (both are ), we can set the exponents equal to each other for the equation to hold true. Therefore, must be equal to .
- Error Checking: We check for any mathematical errors in the previous steps. The steps followed the rules of exponents correctly, and there were no arithmetic errors.
More problems from Factor sums and differences of cubes
QuestionGet tutor help
QuestionGet tutor help