Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

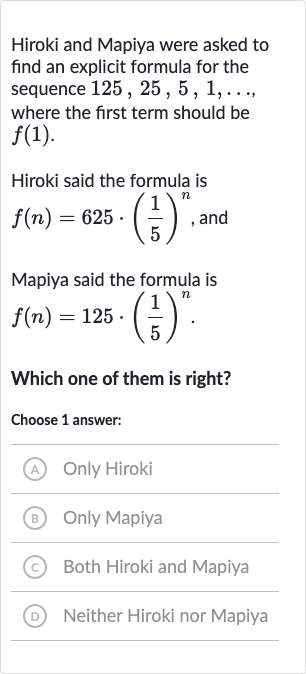
Hiroki and Mapiya were asked to find an explicit formula for the sequence 125,25,5,1,dots, where the first term should be f(1). Hiroki said the formula is f(n)=625*((1)/(5))^(n), and Mapiya said the formula is f(n)=125*((1)/(5))^(n). Which one of them is right? Choose 1 answer: (A) Only Hiroki (B) Only Mapiya (c) Both Hiroki and Mapiya (D) Neither Hiroki nor Mapiya

Hiroki and Mapiya were asked to find an explicit formula for the sequence \newline125,25,5,1,…125, 25, 5, 1, \dots, where the first term should be \newlinef(1)f(1).\newlineHiroki said the formula is \newlinef(n)=625⋅(15)nf(n) = 625 \cdot \left(\frac{1}{5}\right)^n, and\newlineMapiya said the formula is \newlinef(n)=125⋅(15)nf(n) = 125 \cdot \left(\frac{1}{5}\right)^n.\newlineWhich one of them is right?\newlineChoose 11 answer:\newline(A) Only Hiroki\newline(B) Only Mapiya\newline(C) Both Hiroki and Mapiya\newline(D) Neither Hiroki nor Mapiya

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Write variable expressions for geometric sequencesright chevron icon

Full solution

Q. Hiroki and Mapiya were asked to find an explicit formula for the sequence \newline125,25,5,1,…125, 25, 5, 1, \dots, where the first term should be \newlinef(1)f(1).\newlineHiroki said the formula is \newlinef(n)=625⋅(15)nf(n) = 625 \cdot \left(\frac{1}{5}\right)^n, and\newlineMapiya said the formula is \newlinef(n)=125⋅(15)nf(n) = 125 \cdot \left(\frac{1}{5}\right)^n.\newlineWhich one of them is right?\newlineChoose 11 answer:\newline(A) Only Hiroki\newline(B) Only Mapiya\newline(C) Both Hiroki and Mapiya\newline(D) Neither Hiroki nor Mapiya
  1. Identify the pattern: We have the sequence: 125,25,5,1,…125, 25, 5, 1, \ldots\newlineIdentify the pattern in the sequence.
  2. Determine first term and common ratio: The sequence is geometric because each term is obtained by multiplying the previous term by a common ratio.\newlineDetermine the first term (f(1)f(1)) and the common ratio (rr).\newlineFirst term: f(1)=125f(1) = 125\newlineCommon ratio: r=25125=15r = \frac{25}{125} = \frac{1}{5}
  3. Test Hiroki's formula: Now, let's check Hiroki's formula: f(n)=625×(15)nf(n) = 625 \times \left(\frac{1}{5}\right)^n\newlineTest Hiroki's formula with n=1n = 1 to see if it gives the first term of the sequence.\newlinef(1)=625×(15)1=625×15=125f(1) = 625 \times \left(\frac{1}{5}\right)^1 = 625 \times \frac{1}{5} = 125\newlineHiroki's formula gives the correct first term.
  4. Test Mapiya's formula: Next, let's check Mapiya's formula: f(n)=125⋅(15)nf(n) = 125 \cdot \left(\frac{1}{5}\right)^n\newlineTest Mapiya's formula with n=1n = 1 to see if it gives the first term of the sequence.\newlinef(1)=125⋅(15)1=125⋅15=25f(1) = 125 \cdot \left(\frac{1}{5}\right)^1 = 125 \cdot \frac{1}{5} = 25\newlineMapiya's formula does not give the correct first term.
  5. Conclusion: Since Hiroki's formula gives the correct first term and follows the pattern of the sequence, Hiroki is correct.\newlineMapiya's formula does not give the correct first term, so Mapiya is incorrect.

More problems from Write variable expressions for geometric sequences

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 5 months ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 5 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 5 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 7 months ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 9 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 5 months ago

View all (52)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant