Full solution
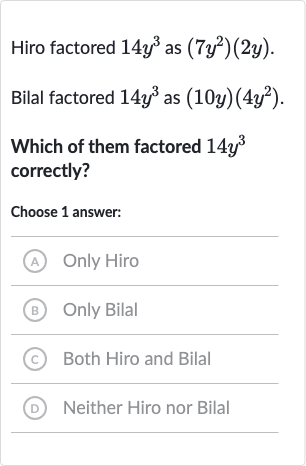
Q. Hiro factored as .Bilal factored as .Which of them factored correctly?Choose answer:(A) Only Hiro(B) Only Bilal(C) Both Hiro and Bilal(D) Neither Hiro nor Bilal
- Identify original expression: Identify the original expression that needs to be factored.The original expression is .
- Check Hiro's factorization: Check Hiro's factorization.Hiro factored as .Multiply Hiro's factors to see if they equal the original expression: .
- Check Bilal's factorization: Check Bilal's factorization.Bilal factored as .Multiply Bilal's factors to see if they equal the original expression: , which is not equal to .
- Determine correct factorization: Determine who factored the expression correctly.Only Hiro's factorization results in the original expression , so Hiro factored it correctly.
More problems from Write variable expressions: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help