AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
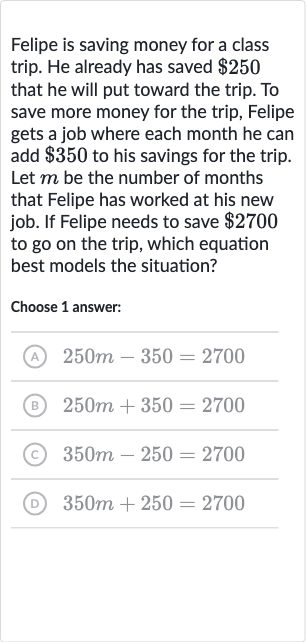
Felipe is saving money for a class trip. He already has saved that he will put toward the trip. To save more money for the trip, Felipe gets a job where each month he can add to his savings for the trip. Let be the number of months that Felipe has worked at his new job. If Felipe needs to save to go on the trip, which equation best models the situation?Choose answer:(A) (B) (C) (D)
Full solution
Q. Felipe is saving money for a class trip. He already has saved that he will put toward the trip. To save more money for the trip, Felipe gets a job where each month he can add to his savings for the trip. Let be the number of months that Felipe has worked at his new job. If Felipe needs to save to go on the trip, which equation best models the situation?Choose answer:(A) (B) (C) (D)
- Initial Amount: Felipe starts with and adds each month for months. We need to find an equation that models the total amount of money Felipe will have after months.
- Monthly Savings: The initial amount Felipe has is . This is a one-time amount and does not change with the number of months.
- Total Savings: Each month, Felipe adds to his savings. So for months, he will add times , which is .
- Equation: The total amount Felipe needs to save is . This total will be the sum of his initial savings and the money he saves from working each month.
- Checking the Equation: The equation that models the situation is the initial savings (m) equals the total needed (\(2700\)). This can be written as: \(250 + 350m = 2700\)
- Checking the Equation: The equation that models the situation is the initial savings (\(250) plus the amount saved each month (\)\(350\)m) equals the total needed (). This can be written as:We can check if this equation matches any of the given options:(A) (Incorrect, this suggests the initial amount is multiplied by the number of months and then \(350\) is subtracted, which does not match the situation.)\(\newline\)(B) \(250m + 350 = 2700\) (Incorrect, this suggests the initial amount is multiplied by the number of months and then is added, which does not match the situation.)(C) (Incorrect, this suggests the amount saved each month is multiplied by the number of months and then the initial savings are subtracted, which does not match the situation.)(D) (Correct, this matches the equation we derived, where the initial savings are added to the amount saved each month.)
