AI tutor
Full solution
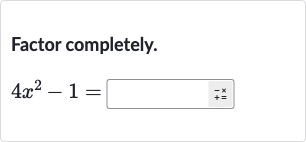
Q. Factor completely.
- Determine factoring technique: Determine the appropriate factoring technique for .Since we have a difference of squares, we can use the identity .
- Identify terms as squares: Identify the terms in the expression as squares. can be written as and can be written as .So, .
- Apply difference of squares formula: Apply the difference of squares formula to factor the expression.Using the identity from Step , we have:.
- Verify no common factors: Verify that there are no common factors and that the expression cannot be factored further.The terms and have no common factors and cannot be factored further.