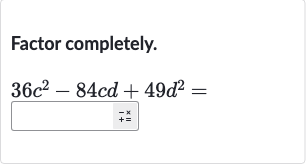Factor completely. 36c^(2)-84 cd+49d^(2)=

Question

Factor completely.  36c^(2)-84 cd+49d^(2)=

Bytelearn · Accepted Answer

Identify Coefficients: Step Title: Identify the Coefficients Concise Step Description: Identify the coefficients of the quadratic equation, which are the numbers in front of the variables. In this case, the coefficients are 36, -84, and 49. Step Calculation: Coefficients are 36, -84, 49 Step Output: Coefficients: 36, -84, 49Check for Common Factor: Step Title: Check for a Common Factor Concise Step Description: Check if there is a common factor that can be factored out from all terms of the quadratic expression. Step Calculation: The greatest common factor of 36, -84, and 49 is 1, so there is no common factor to factor out. Step Output: No common factor to factor out.Recognize Perfect Square Trinomial: Step Title: Recognize the Perfect Square Trinomial Concise Step Description: Determine if the quadratic is a perfect square trinomial, which takes the form (ax)^2 - 2abx + b^2. Step Calculation: The given quadratic is a perfect square trinomial because (6c)^2 = 36c^2, (7d)^2 = 49d^2, and 2*(6c)*(7d) = 84cd. Step Output: The quadratic is a perfect square trinomial.Write Factored Form: Step Title: Write the Factored Form Concise Step Description: Write the factored form of the quadratic equation as a square of a binomial. Step Calculation: The factored form is (6c - 7d)^2. Step Output: Factored Form: (6c - 7d)^2

Factor completely. $\newline$ $36 c^{2}-84 c d+49 d^{2}=$

Full solution

More problems from Factor polynomials

Related topics

Factor completely.\newline36c2−84cd+49d2= 36 c^{2}-84 c d+49 d^{2}= 36c2−84cd+49d2=

Factor completely. $\newline$ $36 c^{2}-84 c d+49 d^{2}=$