AI tutor
Full solution
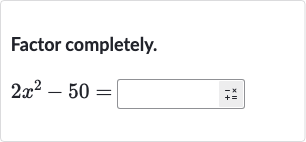
Q. Factor completely.
- Identify common factor: Identify a common factor in the terms and .Both terms are divisible by .Factor out the common factor of .
- Factor out common factor: Recognize that is a difference of squares.So,
- Recognize difference of squares: Apply the difference of squares formula to factor .The difference of squares formula is .
- Apply difference of squares formula: Combine the factored form of with the common factor we factored out in Step .This is the completely factored form of .