AI tutor
Full solution
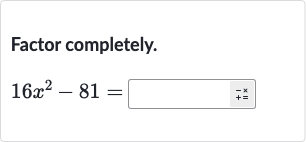
Q. Factor completely.
- Determine Factorization Method: Determine if the expression can be factored using a known method.The expression is a difference of squares because it can be written as , which fits the pattern .
- Write in Form: Write the expression in the form of .So,
- Apply Difference of Squares Formula: Apply the difference of squares formula, which is .
- Write Final Factored Form: Write the final factored form of the expression.The factored form of is .