AI tutor
Full solution
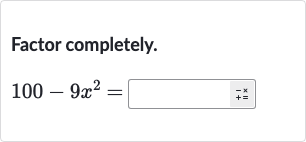
Q. Factor completely.
- Determine the approach: Determine the approach to factor .We can observe that the expression is a difference of squares, which can be factored using the formula .
- Identify in the form: Identify in the form of .So,
- Apply the difference of squares formula: Apply the difference of squares formula to factor the expression.Using the formula , we get: