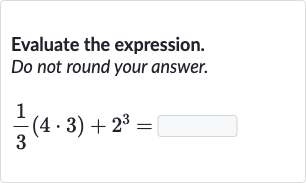
Evaluate the expression. Do not round your answer. (1)/(3)(4*3)+2^(3)=

Question

Evaluate the expression. Do not round your answer.  (1)/(3)(4*3)+2^(3)=

Bytelearn · Accepted Answer

Identify Components: Identify the components of the expression. The expression is (1)/(3)(4*3)+2^(3). It consists of a fraction (1)/(3)(4*3) and an addition of 2^(3).Simplify Fraction: Simplify the fraction part of the expression. The fraction part is (1)/(3)(4*3). First, multiply the numbers in the denominator: 4*3 = 12. Then, the fraction becomes (1)/(3*12).Continue Simplifying: Continue simplifying the fraction. Now, multiply 3*12 to get 36. So, the fraction is (1)/(36).Simplify Exponentiation: Simplify the exponentiation part of the expression. The exponentiation part is 2^(3). Calculate 2^3 = 2*2*2 = 8.Add Results: Add the results of the fraction and the exponentiation. Now, add the simplified fraction (1)/(36) to the result of 2^3, which is 8. So, the expression becomes 1/36 + 8.Convert to Fraction: Convert the whole number to a fraction with the same denominator to add them. To add 8 to 1/36, convert 8 to a fraction with the denominator 36: 8 = 8*(36/36) = 288/36.Add Fractions: Add the two fractions. Now, add 1/36 to 288/36 to get (1 + 288)/36 = 289/36.

Evaluate the expression. Do not round your answer. $\newline$ $\frac{1}{3}(4 \cdot 3)+2^{3}=$

Full solution

More problems from Negative exponents

Related topics

Evaluate the expression. Do not round your answer.\newline13(4⋅3)+23= \frac{1}{3}(4 \cdot 3)+2^{3}= 31​(4⋅3)+23=

Evaluate the expression. Do not round your answer. $\newline$ $\frac{1}{3}(4 \cdot 3)+2^{3}=$