Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

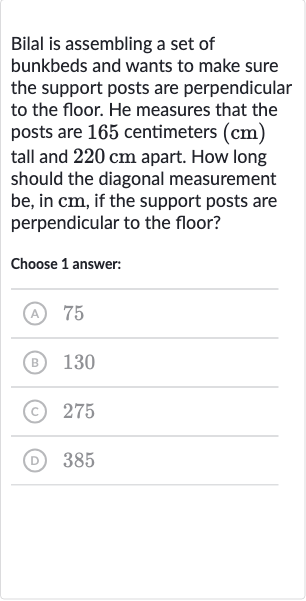
Bilal is assembling a set of bunkbeds and wants to make sure the support posts are perpendicular to the floor. He measures that the posts are 165 centimeters (cm) tall and 220cm apart. How long should the diagonal measurement be, in cm, if the support posts are perpendicular to the floor? Choose 1 answer: (A) 75 (B) 130 (C) 275 (D) 385

Bilal is assembling a set of bunkbeds and wants to make sure the support posts are perpendicular to the floor. He measures that the posts are 165165 centimeters (cm) (\mathrm{cm}) tall and 220 cm 220 \mathrm{~cm} apart. How long should the diagonal measurement be, in cm \mathrm{cm} , if the support posts are perpendicular to the floor?\newlineChoose 11 answer:\newline(A) 7575\newline(B) 130130 \newline(C) 275275\newline(D) 385385

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 6right chevron icon
Solve for a variable using properties of multiplicationright chevron icon

Full solution

Q. Bilal is assembling a set of bunkbeds and wants to make sure the support posts are perpendicular to the floor. He measures that the posts are 165165 centimeters (cm) (\mathrm{cm}) tall and 220 cm 220 \mathrm{~cm} apart. How long should the diagonal measurement be, in cm \mathrm{cm} , if the support posts are perpendicular to the floor?\newlineChoose 11 answer:\newline(A) 7575\newline(B) 130130 \newline(C) 275275\newline(D) 385385
  1. Identify Relationship and Triangle: Identify the relationship between the height of the posts, the distance apart, and the diagonal measurement.\newlineThe posts and the floor form a right-angled triangle, with the posts as one side, the distance between the posts as the base, and the diagonal as the hypotenuse. We can use the Pythagorean theorem to find the length of the diagonal (hypotenuse).
  2. Apply Pythagorean Theorem: Apply the Pythagorean theorem.\newlineThe Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (cc) is equal to the sum of the squares of the other two sides (aa and bb). The formula is c2=a2+b2c^2 = a^2 + b^2.
  3. Plug in Known Values: Plug in the known values into the Pythagorean theorem.\newlineLet's denote the height of the posts as 'aa' (165165 cm), the distance apart as 'bb' (220220 cm), and the diagonal as 'cc'. So we have:\newlinec2=a2+b2c^2 = a^2 + b^2\newlinec2=1652+2202c^2 = 165^2 + 220^2
  4. Calculate Squares: Calculate the squares of the given numbers.\newline1652=27225165^2 = 27225\newline2202=48400220^2 = 48400
  5. Add Squares: Add the squares of the two sides.\newlinec2=27225+48400c^2 = 27225 + 48400\newlinec2=75625c^2 = 75625
  6. Find Square Root: Find the square root of the sum to get the length of the diagonal. \newlinec=75625c = \sqrt{75625}\newlinec=275c = 275
  7. Match with Given Options: Match the calculated diagonal length with the given options.\newlineThe calculated diagonal length is 275 cm275\,\text{cm}, which corresponds to option (C).

More problems from Solve for a variable using properties of multiplication

Question
Simplify the expression:\newline7z2+3z27z^2 + 3z^2 \newline ______
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify the expression:\newline10f+8f−9f−6f10f + 8f - 9f - 6f\newline____
Get tutor helpright-arrow

Posted 7 months ago

Question
Subtract.\newline(3h+6)−(3h+2)(3h + 6) - (3h + 2)\newline____
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify the expression:\newline2p−p2p - p \newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
A school charges $6\$6 per ticket to a dance. They spend $300\$300 on music and decorations. The expression 6n−3006n-300 describes the amount of profit the school makes from the dance if nn students buy tickets. What does 6n6n represent in this context?\newlineChoices:\newline(A)The amount of money the school charges for all `\n` tickets\newline(B)The amount of money the school spends on the dance\newline(C)The number of students who buy tickets\newline(D)The profit the school earns per ticket
Get tutor helpright-arrow

Posted 8 months ago

Question
Which is equal to cos⁡60∘ \cos 60^\circ ? \newlineChoices:\newline(A) sin⁡30∘ \sin 30^\circ \newline(B) sin⁡60∘ \sin 60^\circ \newline(C) cos⁡30∘ \cos 30^\circ \newline(D) cos⁡60∘ \cos 60^\circ
Get tutor helpright-arrow

Posted 9 months ago

Question
Which is equal to sin⁡45∘\sin 45^\circ? \newlineChoices:\newline(A) cos⁡45∘\cos 45^\circ\newline(B) cos⁡55∘\cos 55^\circ\newline(C) sin⁡55∘\sin 55^\circ\newline(D) sin⁡35∘\sin 35^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Which is equal to cos⁡75∘\cos 75^\circ? \newlineChoices:\newline(A) sin⁡15∘\sin 15^\circ\newline(B) sin⁡75∘\sin 75^\circ\newline(C) cos⁡15∘\cos 15^\circ\newline(D) cos⁡25∘\cos 25^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Which is equal to sin⁡30∘ \sin 30^\circ ? \newlineChoices:\newline(A) cos⁡60∘ \cos 60^\circ \newline(B) cos⁡30∘ \cos 30^\circ \newline(C) sin⁡60∘ \sin 60^\circ \newline(D) sin⁡30∘ \sin 30^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Which is equal to cos⁡45∘ \cos 45^\circ ? \newlineChoices:\newline(A) sin⁡45∘ \sin 45^\circ \newline(B) sin⁡55∘ \sin 55^\circ \newline(C) cos⁡55∘ \cos 55^\circ \newline(D) cos⁡35∘ \cos 35^\circ
Get tutor helpright-arrow

Posted 7 months ago

View all (33)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant