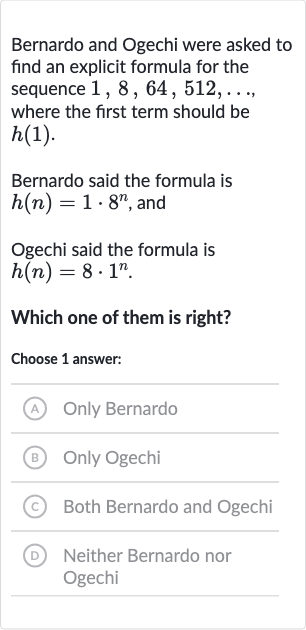
Bernardo and Ogechi were asked to find an explicit formula for the sequence $\newline$ $1,8,64,512,\dots$ , where the first term should be $\newline$ $h(1)$ . $\newline$ Bernardo said the formula is $\newline$ $h(n)=1\times8^{(n-1)}$ , and $\newline$ Ogechi said the formula is $\newline$ $h(n)=8\times1^{(n-1)}$ . $\newline$ Which one of them is right? $\newline$ Choose $1$ answer: $\newline$ (A) Only Bernardo $\newline$ (B) Only Ogechi $\newline$ (C) Both Bernardo and Ogechi $\newline$ (D) Neither Bernardo nor Ogechi

View step-by-step help

Home

Math Problems

Algebra 1

Write variable expressions for geometric sequences

Full solution

Q. Bernardo and Ogechi were asked to find an explicit formula for the sequence

\newline

1,8,64,512,\dots

, where the first term should be

\newline

h(1)

\newline

Bernardo said the formula is

\newline

h(n)=1\times8^{(n-1)}

, and

\newline

Ogechi said the formula is

\newline

h(n)=8\times1^{(n-1)}

\newline

Which one of them is right?

\newline

Choose

1

answer:

\newline

(A) Only Bernardo

\newline

(B) Only Ogechi

\newline

\newline

(D) Neither Bernardo nor Ogechi

Sequence Analysis: We need to analyze the sequence $1, 8, 64, 512, \ldots$ to determine if it is arithmetic or geometric. By looking at the sequence, we can see that each term is multiplied by the same number to get the next term. This indicates that the sequence is geometric.
Finding the Common Ratio: To find the common ratio $r$ , we divide the second term by the first term, the third term by the second term, and so on. Let's calculate the common ratio: $r = \frac{8}{1} = 8$ $r = \frac{64}{8} = 8$ $r = \frac{512}{64} = 8$ Since the common ratio is consistent, we confirm that the sequence is geometric with a common ratio of $8$ .
Confirmation of Geometric Sequence: Now, let's examine Bernardo's formula: $h(n) = 1 \times 8^{(n)}$ . This formula suggests that the first term is $1$ (which is correct) and that the common ratio is $8$ . To check if this formula is correct, we can plug in the position of the terms: $\newline$ For $n = 1$ , $h(1) = 1 \times 8^{(1-1)} = 1 \times 8^0 = 1$ $\newline$ For $n = 2$ , $h(2) = 1 \times 8^{(2-1)} = 1 \times 8^1 = 8$ $\newline$ For $n = 3$ , $h(3) = 1 \times 8^{(3-1)} = 1 \times 8^2 = 64$ $\newline$ This matches the given sequence, so Bernardo's formula appears to be correct.
Examining Bernardo's Formula: Next, let's examine Ogechi's formula: $h(n) = 8 \cdot 1^{(n)}$ . This formula suggests that the first term is $8$ (which is incorrect) and that the common ratio is $1$ . To check if this formula is correct, we can plug in the position of the terms: $\newline$ For $n = 1$ , $h(1) = 8 \cdot 1^{(1-1)} = 8 \cdot 1^0 = 8$ $\newline$ For $n = 2$ , $h(2) = 8 \cdot 1^{(2-1)} = 8 \cdot 1^1 = 8$ $\newline$ For $n = 3$ , $h(3) = 8 \cdot 1^{(3-1)} = 8 \cdot 1^2 = 8$ $\newline$ This does not match the given sequence, so Ogechi's formula is incorrect.
Examining Ogechi's Formula: Since Bernardo's formula correctly represents the sequence and Ogechi's formula does not, the correct answer is that only Bernardo is right.