AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
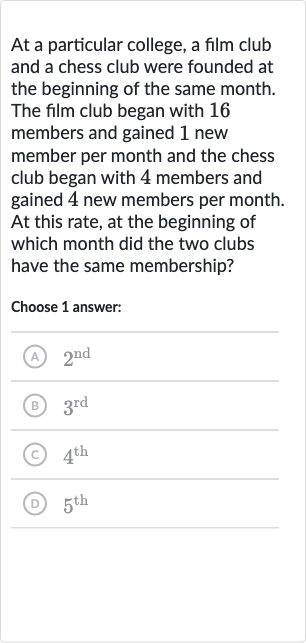
At a particular college, a film club and a chess club were founded at the beginning of the same month. The film club began with members and gained new member per month and the chess club began with members and gained new members per month. At this rate, at the beginning of which month did the two clubs have the same membership?Choose answer:(A) (B) (C) (D)
Full solution
Q. At a particular college, a film club and a chess club were founded at the beginning of the same month. The film club began with members and gained new member per month and the chess club began with members and gained new members per month. At this rate, at the beginning of which month did the two clubs have the same membership?Choose answer:(A) (B) (C) (D)
- Define club members: Let's define the number of members in the film club as and the number of members in the chess club as . Let's also define as the number of months since the clubs were founded. According to the problem, the film club starts with members and gains member per month, so we can express the number of members in the film club as . The chess club starts with members and gains members per month, so we can express the number of members in the chess club as . We want to find the value of when equals .
- Expressing club membership: We set up the equation to find the month when both clubs have the same number of members.
- Setting up the equation: Now we solve for . Subtract from both sides to get .
- Solving for : Next, subtract from both sides to isolate the term with : .
- Finding the value of n: Finally, divide both sides by to solve for n: .
- Conclusion: The value of indicates that at the beginning of the month, the two clubs have the same number of members. Therefore, the correct answer is (C) .
