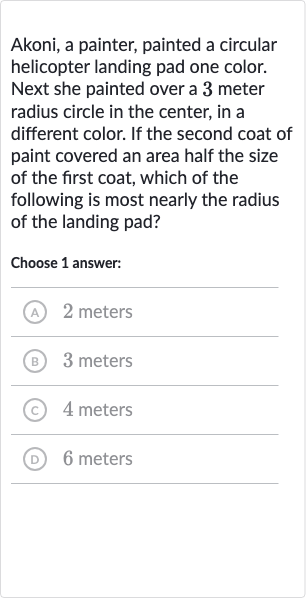
Akoni, a painter, painted a circular helicopter landing pad one color. Next she painted over a 3 meter radius circle in the center, in a different color. If the second coat of paint covered an area half the size of the first coat, which of the following is most nearly the radius of the landing pad? Choose 1 answer: (A) 2 meters (B) 3 meters (C) 4 meters (D) 6 meters

Question

Bytelearn · Accepted Answer

Identify Problem and Values: Understand the problem and identify the known values. Akoni painted a circular helicopter landing pad and then painted over a smaller circle in the center with a different color. The area of the smaller circle is half the size of the larger circle. The radius of the smaller circle is given as 3 meters.Write Area Formula: Write down the formula for the area of a circle. The area of a circle is given by the formula A = πr^2, where A is the area and r is the radius of the circle.Set Up Equation: Set up the equation for the areas of the two circles. Let R be the radius of the larger circle (landing pad). The area of the smaller circle is π(3)^2, and it is half the area of the larger circle, so we have: π(3)^2 = 1/2 * πR^2Simplify and Solve: Simplify the equation and solve for R. 9π = 1/2 * πR^2 To solve for R, we can divide both sides by π and then multiply by 2 to get rid of the fraction: 9 = 1/2 * R^2 18 = R^2Find Radius: Find the value of R by taking the square root of both sides. R = sqrt(18) R ≈ 4.24 metersDetermine Answer Choice: Determine the closest answer choice. The value of R we found is approximately 4.24 meters, which is closest to 4 meters.

Full solution

More problems from Solve a system of equations using substitution: word problems

Related topics