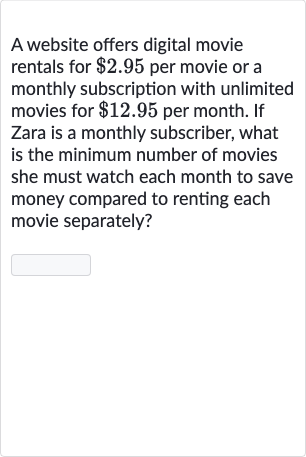
A website offers digital movie rentals for $2.95 per movie or a monthly subscription with unlimited movies for $12.95 per month. If Zara is a monthly subscriber, what is the minimum number of movies she must watch each month to save money compared to renting each movie separately?

Question

A website offers digital movie rentals for  $2.95 per movie or a monthly subscription with unlimited movies for  $12.95 per month. If Zara is a monthly subscriber, what is the minimum number of movies she must watch each month to save money compared to renting each movie separately?

Bytelearn · Accepted Answer

Comparison of Costs: We need to compare the cost of renting movies individually with the cost of the monthly subscription to find the break-even point where Zara starts saving money. Let's denote the number of movies Zara rents as 'n'. The cost of renting 'n' movies individually is $2.95 times 'n'. The cost of the monthly subscription is a flat rate of $12.95. We want to find the smallest integer 'n' such that $2.95n > $12.95.Setting up the Inequality: Set up the inequality to solve for 'n': $2.95n > $12.95.Dividing the Inequality: Divide both sides of the inequality by $2.95 to solve for 'n': n > $12.95 / $2.95.Finding the Value of 'n': Perform the division to find the value of 'n': n > 4.3898... Since Zara can't watch a fraction of a movie, we round up to the next whole number.Rounding up to the Next Whole Number: Zara must watch at least 5 movies to save money with the monthly subscription, as 5 is the smallest whole number greater than 4.3898.

A website offers digital movie rentals for $\$ 2.95$ per movie or a monthly subscription with unlimited movies for $\$ 12.95$ per month. If Zara is a monthly subscriber, what is the minimum number of movies she must watch each month to save money compared to renting each movie separately?

Full solution

More problems from GCF and LCM: word problems

Related topics