Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A line is graphed in the xy-plane shown. Which of the following is an equation of the line, if the line passes through the points (0, 0) and (2, -3) ? Choose 1 answer: (A) y=(3)/(2)x (B) y=(2)/(3)x (C) y=-(3)/(2)x (D) y=-(2)/(3)x

A line is graphed in the xy x y -plane shown. Which of the following is an equation of the line, if the line passes through the points (0,0)(0, 0) and (2,−3)(2, -3)??\newlineChoose 11 answer:\newline(A) y=32x y=\frac{3}{2} x \newline(B) y=23x y=\frac{2}{3} x \newline(C) y=−32x y=-\frac{3}{2} x \newline(D) y=−23x y=-\frac{2}{3} x

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Write a quadratic function from its x-intercepts and another pointright chevron icon

Full solution

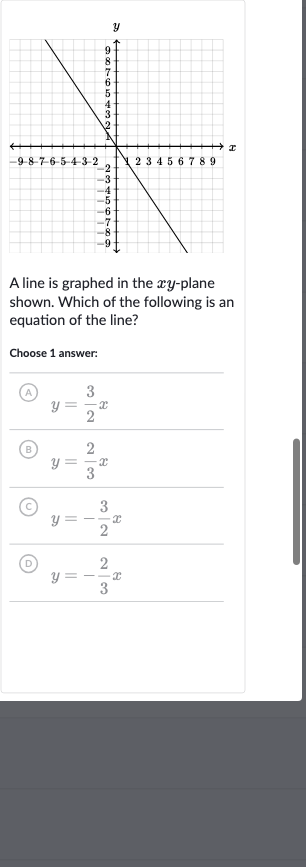
Q. A line is graphed in the xy x y -plane shown. Which of the following is an equation of the line, if the line passes through the points (0,0)(0, 0) and (2,−3)(2, -3)??\newlineChoose 11 answer:\newline(A) y=32x y=\frac{3}{2} x \newline(B) y=23x y=\frac{2}{3} x \newline(C) y=−32x y=-\frac{3}{2} x \newline(D) y=−23x y=-\frac{2}{3} x
  1. Calculate the slope: To find the equation of the line, we first need to calculate the slope mm using the two given points (0,0)(0, 0) and (2,−3)(2, -3). The slope is given by the formula m=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}.
  2. Substitute coordinates into slope formula: Substitute the coordinates of the points into the slope formula: m=−3−02−0=−32m = \frac{-3 - 0}{2 - 0} = \frac{-3}{2}.
  3. Determine the y-intercept: The slope of the line is m=−32m = -\frac{3}{2}. Since the line passes through the origin (0,0)(0, 0), the y-intercept bb is 00. Therefore, the equation of the line in slope-intercept form y=mx+by = mx + b is y=−32x+0y = -\frac{3}{2}x + 0, which simplifies to y=−32xy = -\frac{3}{2}x.
  4. Write the equation in slope-intercept form: Now we compare the equation y=−32xy = -\frac{3}{2}x with the given options to find the correct one. The correct option is (C) y=−32xy = -\frac{3}{2}x.

More problems from Write a quadratic function from its x-intercepts and another point

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 1 year ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 9 months ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 9 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 9 months ago

View all (106)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant