Full solution
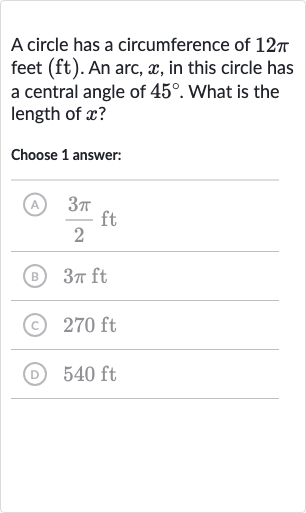
Q. A circle has a circumference of feet . An arc, , in this circle has a central angle of . What is the length of ?Choose answer:(A) (B) (C) (D)
- Convert to Fraction: To find the length of an arc in a circle, we can use the formula arc length = * circumference. The central angle is given as degrees, and the circumference is given as feet.
- Calculate Arc Length: First, we need to convert the central angle from degrees to a fraction of a full circle. Since a full circle is degrees, a -degree angle is of a full circle.
- Simplify Fraction: Now, we can calculate the arc length by multiplying the fraction of the circle that the angle represents by the total circumference. So, the arc length .
- Multiply by Circumference: Simplify the fraction by dividing both the numerator and the denominator by . This gives us .
- Simplify Expression: Now, multiply the simplified fraction by the circumference: .
- Final Arc Length: Simplify the expression by dividing by , which gives us .
- Final Arc Length: Simplify the expression by dividing by , which gives us .The length of the arc is therefore feet, which can also be written as feet.