Full solution
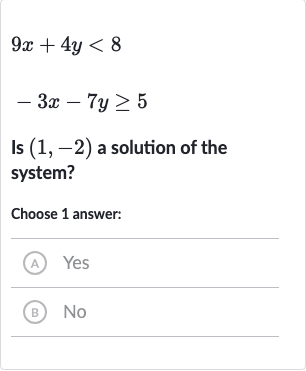
Q. Is a solution of the system?Choose answer:(A) Yes(B) No
- Step : Check first inequality: Check if the point satisfies the inequality 9x + 4y < 8.Substitute and into the inequality 9x + 4y < 8.9(1) + 4(-2) < 89 - 8 < 81 < 8The point satisfies the first inequality.
- Step : Check second inequality: Check if the point satisfies the inequality .Substitute and into the inequality .The point satisfies the second inequality.
- Step : Determine solution to the system: Determine if the point is a solution to the system of inequalities.Since the point satisfies both inequalities, it is a solution to the system.