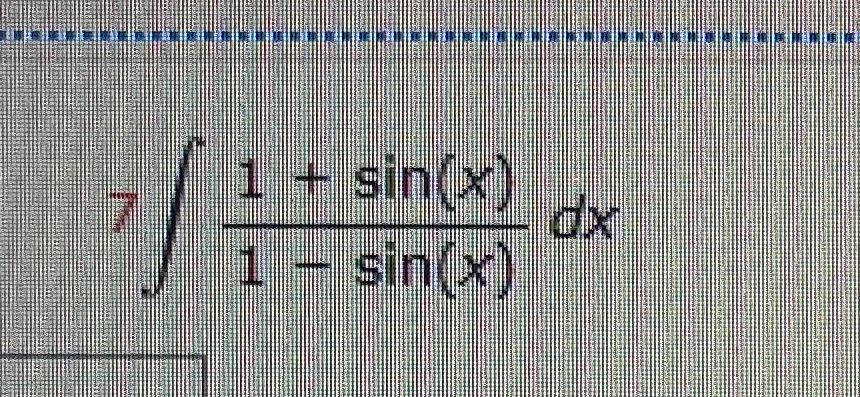AI tutor
Full solution
Q.
- Identify Integral: Identify the integral to be solved.We need to find the integral of the function with respect to .
- Simplify Integrand: Simplify the integrand if possible.In this case, we can try to simplify the integrand by using a trigonometric identity or by manipulating the expression. However, the expression does not simplify easily using basic trigonometric identities.
- Use Substitution: Use substitution to simplify the integral.Let's use the substitution method. We can let , which means . We need to express everything in the integral in terms of , including .
- Find : Find in terms of .Since , we can solve for . .
- Substitute and : Substitute and into the integral.Substituting and into the integral, we get:
- Express : Express in terms of . We have , so . Now we can substitute this into the integral.
- Substitute : Substitute with in the integral.After substitution, the integral becomes:
- Simplify Integrand: Simplify the integrand.Simplify the expression inside the integral:
- Realize Mistake: Realize there is a mistake in the substitution.We made a mistake in the substitution process. The correct substitution should have been:However, we cannot proceed because we have not expressed in terms of , which is necessary to complete the substitution. We need to go back and correct this.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help