AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
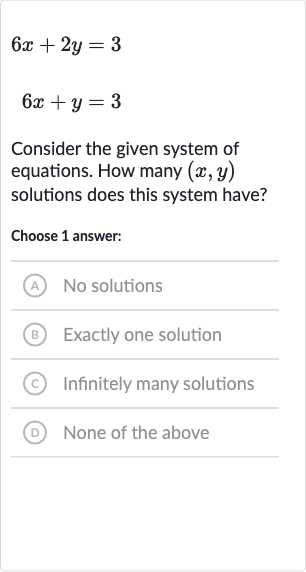
Consider the given system of equations. How many solutions does this system have?Choose answer:(A) No solutions(B) Exactly one solution(C) Infinitely many solutions(D) None of the above
Full solution
Q. Consider the given system of equations. How many solutions does this system have?Choose answer:(A) No solutions(B) Exactly one solution(C) Infinitely many solutions(D) None of the above
- Analyze Equations: Analyze the given system of equations.We have two linear equations:) ) We will compare the coefficients of and in both equations to determine if they are parallel, the same line, or intersecting lines.
- Compare Equations: Compare the two equations.If we multiply the second equation by , we get:Which simplifies to:Now, we compare this with the first equation:We can see that the coefficients of and are the same in both equations, but the constants on the right side are different. This means the lines are parallel and do not intersect.
- Conclude Solutions: Conclude the number of solutions.Since the lines are parallel and have different -intercepts, they will never intersect. Therefore, there are no solutions to this system of equations.
More problems from Solve trigonometric equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help
