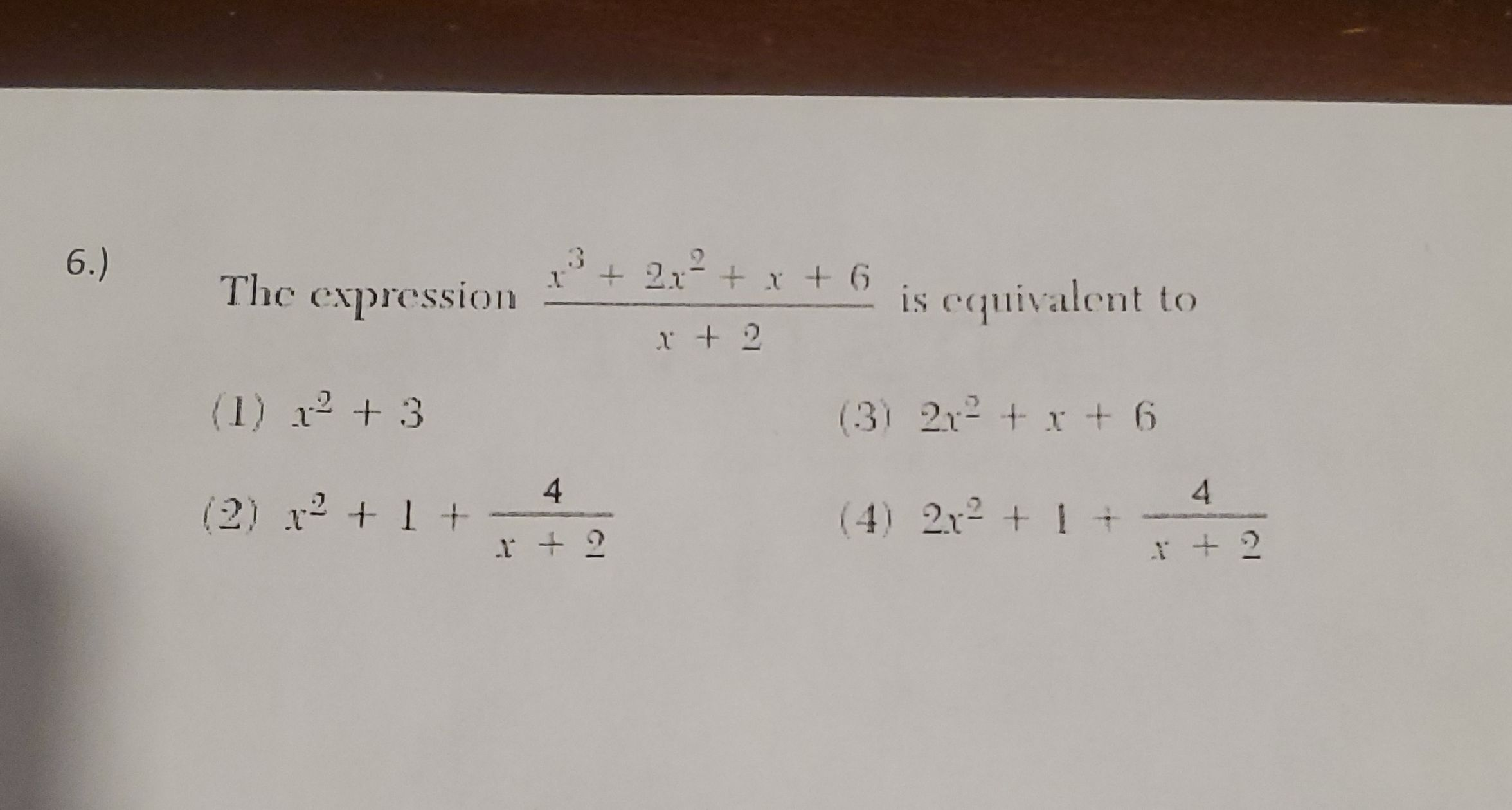6.) The expression (x^(3)+2x^(2)+x+6)/(x+2) is equivalent to (1) x^(2)+3 (3) 2x^(2)+x+6 (2) x^(2)+1+(4)/(x+2) (4) 2x^(2)+1+(4)/(x+2)

Question

6.) The expression  (x^(3)+2x^(2)+x+6)/(x+2) is equivalent to (1)  x^(2)+3 (3)  2x^(2)+x+6 (2)  x^(2)+1+(4)/(x+2) (4)  2x^(2)+1+(4)/(x+2)

Bytelearn · Accepted Answer

Perform Division: Perform polynomial long division or synthetic division to simplify the expression. We will divide the polynomial x^3 + 2x^2 + x + 6 by x + 2.Set Up: Set up the division. Write x^3 + 2x^2 + x + 6 under the division bar and x + 2 outside the division bar.Divide First Term: Divide the first term of the dividend by the first term of the divisor. Divide x^3 by x to get x^2. Write x^2 above the division bar.Multiply and Subtract: Multiply the divisor by the result from the previous step. Multiply x + 2 by x^2 to get x^3 + 2x^2. Write this result under the corresponding terms of the dividend.Repeat Division: Subtract the result from the previous step from the dividend. Subtract (x^3 + 2x^2) from (x^3 + 2x^2) to get 0. Bring down the next term of the dividend, which is x.Divide Next Term: Repeat the division process with the new dividend. Divide x by x to get 1. Write 1 above the division bar next to x^2.Multiply and Subtract: Multiply the divisor by the result from the previous step. Multiply x + 2 by 1 to get x + 2. Write this result under the corresponding terms of the new dividend.Repeat Division: Subtract the result from the previous step from the new dividend. Subtract (x + 2) from (x) to get -2. Bring down the next term of the dividend, which is 6.Add Final Term: Repeat the division process with the new dividend. Divide -2 by x to get 0, since -2 cannot be divided by x to give a polynomial term. Write 0 above the division bar next to 1.Write Final Result: Add the final term of the dividend to the remainder. The remainder is now -2 + 6, which simplifies to 4.Match with Options: Write the final result of the division. The quotient is x^2 + 1, and the remainder is 4. The expression can be written as x^2 + 1 + 4/(x + 2).Match the result with the given options. The equivalent expression is x^2 + 1 + 4/(x + 2), which corresponds to option (2).

The expression $\frac{x^{3}+2 x^{2}+x+6}{x+2}$ is equivalent to $\newline$ ( $1$ ) $x^{2}+3$ $\newline$ ( $3$ ) $2 x^{2}+x+6$ $\newline$ ( $2$ ) $x^{2}+1+\frac{4}{x+2}$ $\newline$ ( $4$ ) $2 x^{2}+1+\frac{4}{x+2}$

Full solution

More problems from Multiplication with rational exponents

Related topics

The expression x3+2x2+x+6x+2 \frac{x^{3}+2 x^{2}+x+6}{x+2} x+2x3+2x2+x+6​ is equivalent to\newline(111) x2+3 x^{2}+3 x2+3\newline(333) 2x2+x+6 2 x^{2}+x+6 2x2+x+6\newline(222) x2+1+4x+2 x^{2}+1+\frac{4}{x+2} x2+1+x+24​\newline(444) 2x2+1+4x+2 2 x^{2}+1+\frac{4}{x+2} 2x2+1+x+24​

The expression $\frac{x^{3}+2 x^{2}+x+6}{x+2}$ is equivalent to $\newline$ ( $1$ ) $x^{2}+3$ $\newline$ ( $3$ ) $2 x^{2}+x+6$ $\newline$ ( $2$ ) $x^{2}+1+\frac{4}{x+2}$ $\newline$ ( $4$ ) $2 x^{2}+1+\frac{4}{x+2}$