AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
markers cost .Which equation would help determine the cost of markers?Choose answer:(A) (B) (C) (D) (E) None of the above
Full solution
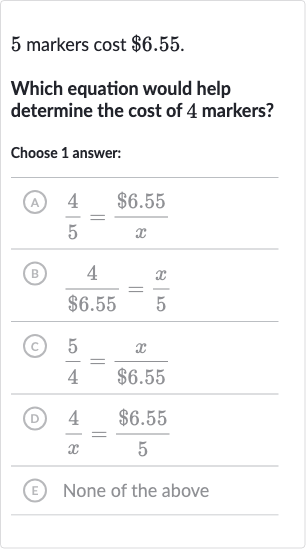
Q. markers cost .Which equation would help determine the cost of markers?Choose answer:(A) (B) (C) (D) (E) None of the above
- Denote Cost of One Marker: Let's denote the cost of one marker as . We know that markers cost $\(6\).\(55\). Therefore, we can write the equation for the cost of \(5\) markers as \( 5c = 6.55 \). To find the cost of \(4\) markers, we need to find \( 4c \). We can set up a proportion where the number of markers is directly proportional to the total cost. The equation should relate the cost of \(4\) markers to the cost of \(5\) markers.
- Set Up Proportion: We can set up the proportion as follows: \( \frac{4}{5} = \frac{x}{6.55} \), where \( x \) represents the cost of \(4\) markers. This equation states that the ratio of the cost of \(4\) markers to the cost of \(5\) markers is the same as the ratio of the number of markers (\(4\) to \(5\)). This is the correct setup for a proportion.
- Analyze Answer Choices: Looking at the given answer choices, we see that option (A) \( \frac{4}{5} = \frac{6.55}{x} \) incorrectly suggests that the cost of \(5\) markers is inversely proportional to the cost of \(4\) markers, which is not the case. Option (B) \( \frac{4}{6.55} = \frac{x}{5} \) also incorrectly sets up the proportion by suggesting that the number of markers is inversely proportional to the cost. Option (C) \( \frac{5}{4} = \frac{x}{6.55} \) incorrectly inverts the ratio of markers. Option (D) \( \frac{4}{x} = \frac{6.55}{5} \) incorrectly suggests that the cost of \(4\) markers is inversely proportional to the number of markers. Therefore, none of the given options correctly represent the proportion we need.
