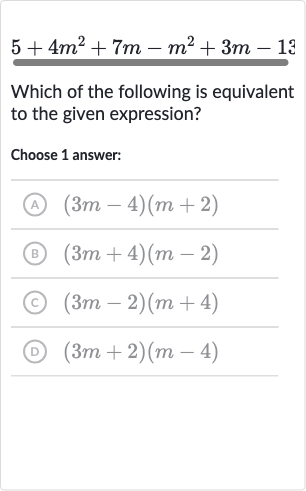
5+4m^(2)+7m-m^(2)+3m-13 Which of the following is equivalent to the given expression? Choose 1 answer: (A) (3m-4)(m+2) (B) (3m+4)(m-2) (C) (3m-2)(m+4) (D) (3m+2)(m-4)

Question

5+4m^(2)+7m-m^(2)+3m-13 Which of the following is equivalent to the given expression? Choose 1 answer: (A)  (3m-4)(m+2) (B)  (3m+4)(m-2) (C)  (3m-2)(m+4) (D)  (3m+2)(m-4)

Bytelearn · Accepted Answer

Rephrase Question: First, let's rephrase the  ＂What is the equivalent expression for the given algebraic expression?＂Combine Like Terms: Combine like terms in the expression 5 + 4m^2 + 7m - m^2 + 3m - 13. 4m^2 - m^2 = 3m^2 (combining the m^2 terms) 7m + 3m = 10m (combining the m terms) 5 - 13 = -8 (combining the constant terms) So the simplified expression is 3m^2 + 10m - 8.Factor Simplified Expression: Now, we need to factor the simplified expression 3m^2 + 10m - 8. We are looking for two numbers that multiply to (3m^2)(-8) = -24m^2 and add up to 10m.Find Factors: The two numbers that meet these criteria are 12m and -2m because 12m * -2m = -24m^2 and 12m + -2m = 10m. So we can write the expression as 3m^2 + 12m - 2m - 8.Group and Factor: Now, we factor by grouping. Group the first two terms and the last two terms: (3m^2 + 12m) + (-2m - 8) Factor out the common factor from each group: 3m(m + 4) - 2(m + 4)Common Factor: Since both terms have a common factor of (m + 4), we can factor it out: (3m - 2)(m + 4)Compare and Choose: We compare the factored expression (3m - 2)(m + 4) with the answer choices: (A) (3m - 4)(m + 2) (B) (3m + 4)(m - 2) (C) (3m - 2)(m + 4) (D) (3m + 2)(m - 4) The correct answer is (C) (3m - 2)(m + 4).

$5+4 m^{2}+7 m-m^{2}+3 m-13$ $\newline$ Which of the following is equivalent to the given expression? $\newline$ Choose $1$ answer: $\newline$ (A) $(3 m-4)(m+2)$ $\newline$ (B) $(3 m+4)(m-2)$ $\newline$ (C) $(3 m-2)(m+4)$ $\newline$ (D) $(3 m+2)(m-4)$

Full solution

More problems from Simplify rational expressions

Related topics