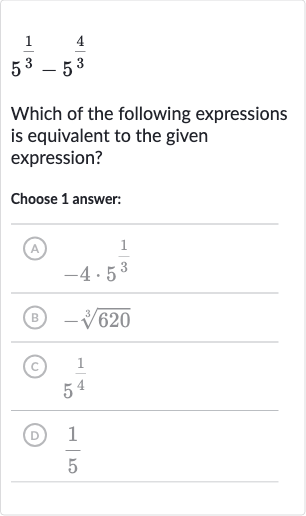
Full solution
Q. Which of the following expressions is equivalent to the given expression?Choose answer:(A) ( (C) (D)
- Analyze given expression: First, let's analyze the given expression: . We notice that both terms have the base of , but different exponents. The second term can be rewritten using the property of exponents that states . So, is the same as .
- Rewrite second term: Now, let's rewrite the second term using the property mentioned above: . Since , we can substitute this into our expression: .
- Recognize cube root: We recognize that is the cube root of . The cube root of is , which is . Therefore, .
- Factor out common term: Substituting back into our expression, we have: . We can factor out from both terms, which gives us: .
- Simplify expression: Now, we simplify the expression inside the parentheses: equals . So, our expression becomes: .
- Simplify expression: Now, we simplify the expression inside the parentheses: equals . So, our expression becomes: .We have now simplified the original expression to , which matches choice (A) from the provided options.