Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

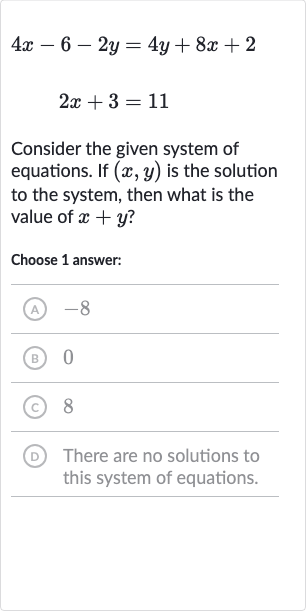
4x-6-2y=4y+8x+2

2x+3=11
Consider the given system of equations. If
(x,y) is the solution to the system, then what is the value of
x+y ?
Choose 1 answer:
(A) -8
(B) 0
(c) 8
(D) There are no solutions to this system of equations.

$4 x-6-2 y=4 y+8 x+2$ $\newline$ $2 x+3=11$ $\newline$ Consider the given system of equations. If $(x, y)$ is the solution to the system, then what is the value of $x+y$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $-8$ $\newline$ (B) $0$ $\newline$ (C) $8$ $\newline$ D There are no solutions to this system of equations.

View step-by-step help

View step-by-step help

Solve rational equations

Full solution

Q.

4 x-6-2 y=4 y+8 x+2

\newline

2 x+3=11

\newline

Consider the given system of equations. If

(x, y)

is the solution to the system, then what is the value of

x+y

?

\newline

Choose

1

answer:

\newline

(A)

-8

\newline

(B)

0

\newline

(C)

8

\newline

D There are no solutions to this system of equations.

Solve for x: First, let's solve the second equation for x. $\newline$ The equation is $2x + 3 = 11$ . $\newline$ Subtract $3$ from both sides to isolate the term with $x$ . $\newline$ $2x + 3 - 3 = 11 - 3$ $\newline$ $2x = 8$ $\newline$ Now, divide both sides by $2$ to solve for $x$ . $\newline$ $\frac{2x}{2} = \frac{8}{2}$ $\newline$ $x = 4$
Substitute $x$ into first equation: Next, we substitute the value of $x$ into the first equation to solve for $y$ . The first equation is $4x - 6 - 2y = 4y + 8x + 2$ . $\newline$ Substitute $x = 4$ into the equation. $\newline$ $4(4) - 6 - 2y = 4y + 8(4) + 2$ $\newline$ $16 - 6 - 2y = 4y + 32 + 2$ $\newline$ Simplify both sides. $\newline$ $10 - 2y = 4y + 34$
Get y terms on one side: Now, let's get all the y terms on one side and the constants on the other side. $\newline$ Add $2y$ to both sides and subtract $34$ from both sides. $\newline$ $10 - 2y + 2y - 34 = 4y + 2y + 34 - 34$ $\newline$ Combine like terms. $\newline$ $-24 = 6y$ $\newline$ Now, divide both sides by $6$ to solve for y. $\newline$ $\frac{-24}{6} = \frac{6y}{6}$ $\newline$ $y = -4$
Find $x + y$ : Finally, we find the value of $x + y$ . $\newline$ We have $x = 4$ and $y = -4$ . $\newline$ $x + y = 4 + (-4)$ $\newline$ $x + y = 0$

More problems from Solve rational equations

Question

Evaluate the expression for

t = -4.4

\newline

Write your answer in simplest form.

\newline

` frac{t - 4}{t - 2} =` ____

Posted 1 month ago

Question

Simplify. Write your answer using whole numbers and variables.

\newline

\frac{g}{3g^2 - 4g}

Posted 2 months ago

Question

Simplify. Express your answer as a single fraction in simplest form.

\frac{3}{2} - \frac{5p^3}{3}

Posted 2 months ago

Question

Simplify. Express your answer as a single fraction in simplest form.

\newline

\frac{1 + \frac{v^5w}{3}}{1}

\newline

Posted 2 months ago

Question

h

\newline

\frac{-5}{h - 2} = \frac{-4}{h - 3}

\newline

1

2

\newline

h =

h =

Posted 1 month ago

Question

What is the equation of the vertical asymptote of

y = \frac{1}{x + 9}

Posted 2 months ago

Question

What is the excluded value for

y = \frac{1}{x - 9} - 9

\newline

Posted 2 months ago

Question

Simplify. Write your answer using whole numbers and variables.

\newline

\frac{9k + 4}{9k^2 + 4k}

\newline

Posted 2 months ago

Question

Divide. Write your answer in simplest form.

\newline

\frac{g- 1}{10g^3 + 25g^2} \div (g- 1)

\newline

Posted 2 months ago

Question

Simplify. Express your answer as a single fraction in simplest form.

\newline

\frac{5 - \frac{3}{t^3}}{1}

\newline

Posted 2 months ago