Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

4n-30=2(2n+15)
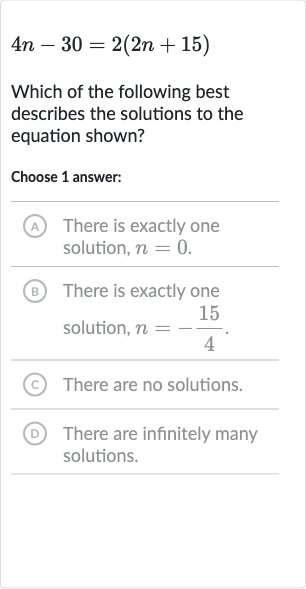
Which of the following best describes the solutions to the equation shown?
Choose 1 answer:
A There is exactly one solution,
n=0.
(B) There is exactly one solution,
n=-(15)/(4).
(c) There are no solutions.
(D) There are infinitely many solutions.

$4n-30=2(2n+15)$ $\newline$ Which of the following best describes the solutions to the equation shown? $\newline$ Choose $1$ answer: $\newline$ A) There is exactly one solution, $n=0$ . $\newline$ (B) There is exactly one solution, $n=-\frac{15}{4}$ . $\newline$ (C) There are no solutions. $\newline$ (D) There are infinitely many solutions.

View step-by-step help

View step-by-step help

Solve rational equations

Full solution

Q.

4n-30=2(2n+15)

\newline

Which of the following best describes the solutions to the equation shown?

\newline

Choose

1

answer:

\newline

A) There is exactly one solution,

n=0

.

\newline

(B) There is exactly one solution,

n=-\frac{15}{4}

.

\newline

(C) There are no solutions.

\newline

(D) There are infinitely many solutions.

Rephrasing the equation: First, let's rephrase the ＂What is the solution to the equation $4n - 30 = 2(2n + 15)$ ?＂
Expanding the right side: Now, let's solve the equation step by step. We start by expanding the right side of the equation where the expression $2(2n + 15)$ is. $4n - 30 = 2 \times 2n + 2 \times 15$
Simplifying the equation: Simplify the right side of the equation by multiplying the terms inside the parentheses by $2$ . $\newline$ $4n - 30 = 4n + 30$
Isolating the variable: Next, we will try to isolate the variable $n$ on one side of the equation. However, we notice that we have the same term $4n$ on both sides of the equation. Let's subtract $4n$ from both sides to see what happens. $\newline$ $4n - 4n - 30 = 4n - 4n + 30$
Subtracting $4n$ from both sides: After subtracting $4n$ from both sides, we get: $\newline$ $0 - 30 = 0 + 30$ $\newline$ $-30 = 30$
Arriving at a contradiction: We have arrived at a contradiction, $-30$ does not equal $30$ . This means that there are no values of $n$ that will satisfy the equation. Therefore, there are no solutions to the equation.

More problems from Solve rational equations

Question

Evaluate the expression for

t = -4.4

\newline

Write your answer in simplest form.

\newline

` frac{t - 4}{t - 2} =` ____

Posted 1 month ago

Question

Simplify. Write your answer using whole numbers and variables.

\newline

\frac{g}{3g^2 - 4g}

Posted 2 months ago

Question

Simplify. Express your answer as a single fraction in simplest form.

\frac{3}{2} - \frac{5p^3}{3}

Posted 2 months ago

Question

Simplify. Express your answer as a single fraction in simplest form.

\newline

\frac{1 + \frac{v^5w}{3}}{1}

\newline

Posted 2 months ago

Question

h

\newline

\frac{-5}{h - 2} = \frac{-4}{h - 3}

\newline

1

2

\newline

h =

h =

Posted 1 month ago

Question

What is the equation of the vertical asymptote of

y = \frac{1}{x + 9}

Posted 2 months ago

Question

What is the excluded value for

y = \frac{1}{x - 9} - 9

\newline

Posted 2 months ago

Question

Simplify. Write your answer using whole numbers and variables.

\newline

\frac{9k + 4}{9k^2 + 4k}

\newline

Posted 2 months ago

Question

Divide. Write your answer in simplest form.

\newline

\frac{g- 1}{10g^3 + 25g^2} \div (g- 1)

\newline

Posted 2 months ago

Question

Simplify. Express your answer as a single fraction in simplest form.

\newline

\frac{5 - \frac{3}{t^3}}{1}

\newline

Posted 2 months ago